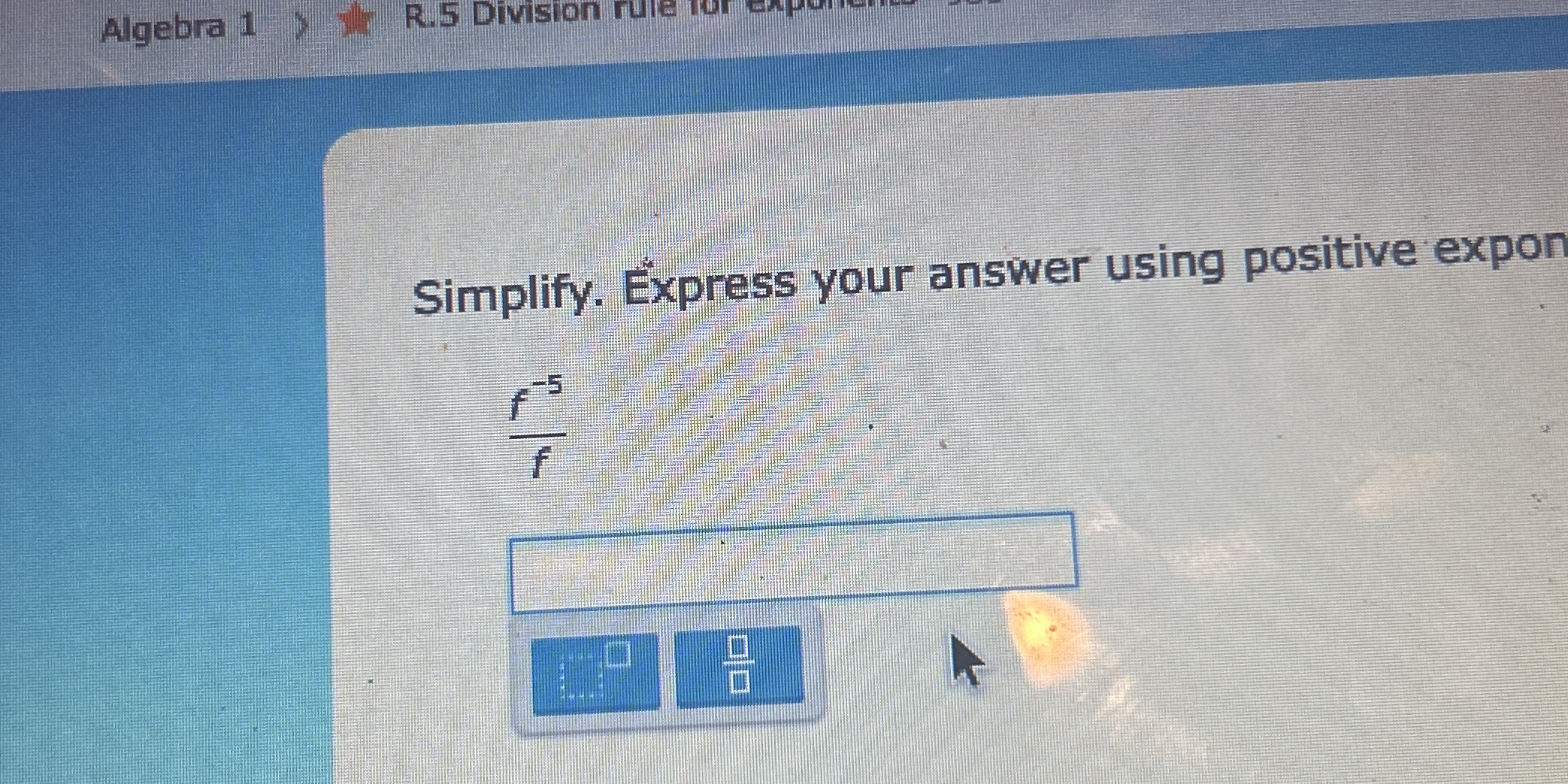
Simplify f^{-5} / f and express your answer using positive exponents.
Understand the Problem
The question is asking to simplify the expression f^{-5} / f and express the result using positive exponents.
Answer
The simplified expression is $\frac{1}{f^6}$.
Answer for screen readers
The simplified expression is $\frac{1}{f^6}$.
Steps to Solve
- Rewrite the Division of Exponents
Using the rule of exponents that states $\frac{a^m}{a^n} = a^{m-n}$, rewrite the expression:
$$ \frac{f^{-5}}{f} = f^{-5 - 1} $$
- Combine the Exponents
Now combine the exponents:
$$ f^{-5 - 1} = f^{-6} $$
- Convert to Positive Exponent
To express the result with a positive exponent, recall that $a^{-n} = \frac{1}{a^n}$:
$$ f^{-6} = \frac{1}{f^6} $$
The simplified expression is $\frac{1}{f^6}$.
More Information
Using the rules of exponents allows us to easily simplify complicated expressions. This specific simplification showcases how negative exponents can be transformed into positive exponents by expressing them as fractions.
Tips
- Forgetting to apply the exponent rule $\frac{a^m}{a^n} = a^{m-n}$ correctly.
- Confusing the negative exponent rule; the correct transformation is crucial for accurate results.
AI-generated content may contain errors. Please verify critical information