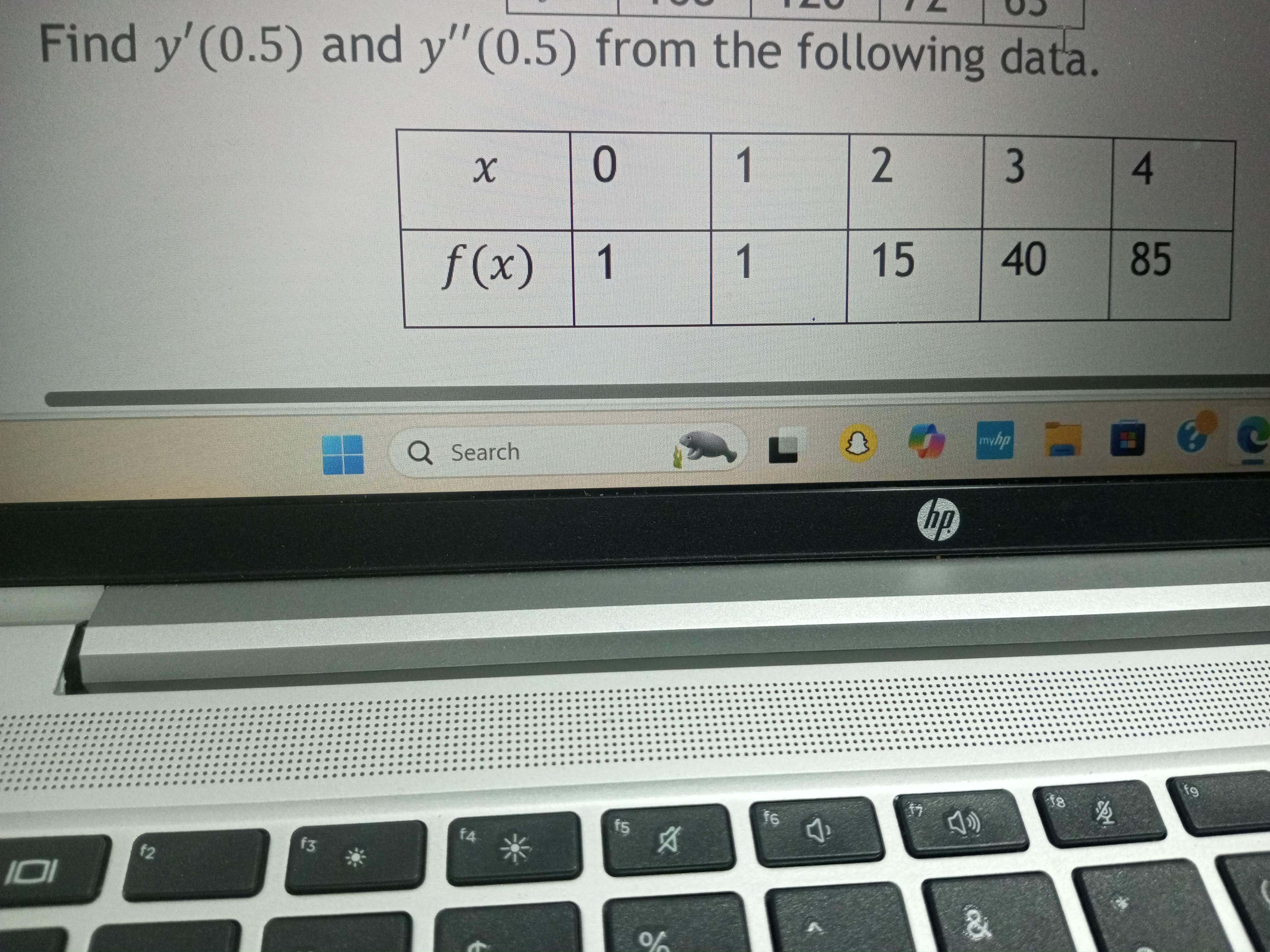
Find y'(0.5) and y''(0.5) from the following data.
Understand the Problem
The question is asking to find the first and second derivatives of the function at x = 0.5 based on the provided data. It requires applying numerical differentiation techniques to estimate these values.
Answer
\( y'(0.5) \approx 19.5 \), \( y''(0.5) \approx 5.5 \)
Answer for screen readers
The first derivative at ( x = 0.5 ) is ( y'(0.5) \approx 19.5 ) and the second derivative is ( y''(0.5) \approx 5.5 ).
Steps to Solve
- Identify the data points
From the given data, we have the following points:
- ( f(0) = 1 )
- ( f(1) = 15 )
- ( f(2) = 40 )
- ( f(3) = 85 )
- ( f(4) = 120 )
- Calculate the first derivative ( y'(0.5) )
We can use the central difference method to estimate the derivative:
$$ y'(0.5) \approx \frac{f(1) - f(0)}{1 - 0} = \frac{15 - 1}{1} = 14 $$
Next, we can utilize points at the left and right of ( 0.5 ):
$$ y'(0.5) \approx \frac{f(1) - f(0)}{1 - 0} + \frac{f(2) - f(1)}{2 - 1} \text{ average} $$
Calculating the average with right points, we find:
$$ y'(0.5) = \frac{14 + (40 - 15)}{2} = \frac{14 + 25}{2} = \frac{39}{2} = 19.5 $$
- Calculate the second derivative ( y''(0.5) )
We use the central difference formula for the second derivative:
$$ y''(0.5) \approx \frac{y'(1) - y'(0)}{1 - 0} $$
Where:
$$ y'(1) = \frac{f(2) - f(0)}{2 - 0} = \frac{40 - 1}{2} = \frac{39}{2} $$
And, similarly,
$$ y'(0) = \frac{f(1) - f(0)}{1 - 0} = \frac{15 - 1}{1} = 14 $$
Now, substituting these values into the second derivative formula:
$$ y''(0.5) \approx \frac{\frac{39}{2} - 14}{1} = \frac{\frac{39 - 28}{2}}{1} = \frac{11}{2} = 5.5 $$
The first derivative at ( x = 0.5 ) is ( y'(0.5) \approx 19.5 ) and the second derivative is ( y''(0.5) \approx 5.5 ).
More Information
The first derivative represents the slope of the function at ( x = 0.5 ), indicating how fast the function is changing. The second derivative provides insight into the curvature of the function at that point.
Tips
- Forgetting to use the average when calculating the first derivative can lead to an incorrect estimate.
- Mixing up the values of the data points can yield inaccurate derivatives.
AI-generated content may contain errors. Please verify critical information