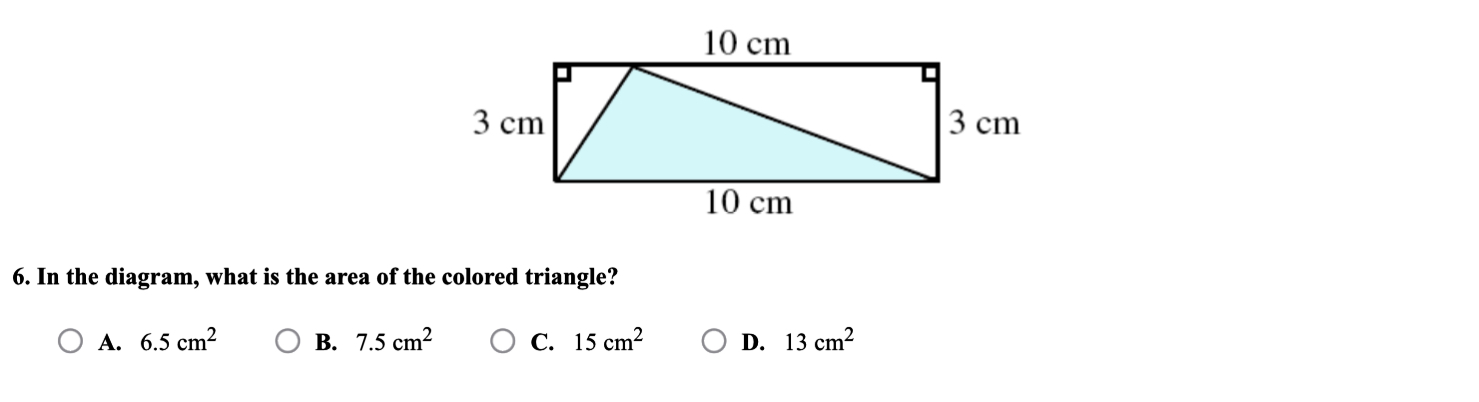
In the diagram, what is the area of the colored triangle?
Understand the Problem
The question asks for the area of a colored triangle within a rectangle, using dimensions provided in the diagram. To solve this, we will use the formula for the area of a triangle, which is (base * height) / 2. Here, the base is identified as part of the rectangle's dimensions, and the height can also be deduced from the dimensions indicated.
Answer
The area of the colored triangle is $15 \, \text{cm}^2$.
Answer for screen readers
The area of the colored triangle is $15 , \text{cm}^2$.
Steps to Solve
-
Identify the dimensions of the triangle The triangle is formed inside the rectangle. We have a rectangle of width $10 , \text{cm}$ and height $3 , \text{cm}$. The triangle has a base equal to the width of the rectangle, which is $10 , \text{cm}$.
-
Determine the height of the triangle The height of the triangle can be inferred from the rectangle. Since the rectangle has a height of $3 , \text{cm}$ and the triangle reaches the bottom edge of the rectangle, the height of the triangle is also $3 , \text{cm}$.
-
Calculate the area of the triangle Using the formula for the area of a triangle:
$$ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} $$
Substituting the values:
- Base = $10 , \text{cm}$
- Height = $3 , \text{cm}$
Thus,
$$ \text{Area} = \frac{1}{2} \times 10 \times 3 = 15 , \text{cm}^2 $$
The area of the colored triangle is $15 , \text{cm}^2$.
More Information
The area calculated corresponds to half the base multiplied by the height of the triangle, which confirms that $15 , \text{cm}^2$ is the total area covered by the triangle. This combination of rectangle dimensions helps in visualizing and solving for triangles within geometric shapes.
Tips
- Misidentifying the base or height of the triangle, especially if the orientation of the triangle is not clear.
- Forgetting to divide by 2 when calculating the area of the triangle.
AI-generated content may contain errors. Please verify critical information