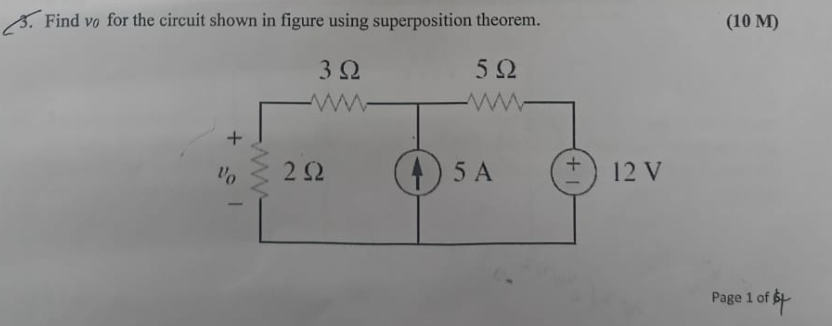
Find v0 for the circuit shown in figure using superposition theorem.

Steps to Solve

1. Identify sources and deactivate others

We have two independent sources: a current source ($5 A$) and a voltage source ($12 V$). To apply the superposition theorem, we analyze the circuit twice—once with the current source active and the voltage source deactivated (replaced with a short circuit), and once with the voltage source active and the current source deactivated (replaced with an open circuit).

2. Calculate voltage $v_0$ with 5 A current source active

Consider the circuit with the $5 A$ current source active. The $2 , \Omega$ and $3 , \Omega$ resistors are in series, which gives a total resistance of: $$ R_{series} = 2 , \Omega + 3 , \Omega = 5 , \Omega $$

Now, use Ohm's law ($V = IR$) to calculate the voltage across the $2 , \Omega$ resistor: $$ v_0 = I \times R_{2 , \Omega} = 5 , A \times 2 , \Omega = 10 , V $$

3. Calculate voltage $v_0$ with 12 V voltage source active

Now consider the circuit with the $12 V$ voltage source active and the $5 A$ current source deactivated (open circuit). The total resistance seen by the voltage source will be the $2 , \Omega$, $3 , \Omega$, and $5 , \Omega$ in series.

Calculate total resistance: $$ R_{total} = 2 , \Omega + 3 , \Omega + 5 , \Omega = 10 , \Omega $$

Using Ohm's law to find the total current from the $12 V$ source: $$ I_{total} = \frac{12 , V}{10 , \Omega} = 1.2 , A $$

Now find the voltage across the $2 , \Omega$ resistor: $$ v_{0, V} = I_{total} \times 2 , \Omega = 1.2 , A \times 2 , \Omega = 2.4 , V $$

4. Combine results from both sources

Using the principle of superposition, the total voltage $v_0$ across the $2 , \Omega$ resistor is the sum of the voltages due to each active source: $$ v_0 = v_{0, I} + v_{0, V} = 10 , V + 2.4 , V = 12.4 , V $$