Find the volume of the tetrahedron bounded by the planes x + 2y + z = 2, x = 2y, x = 0, and z = 0.
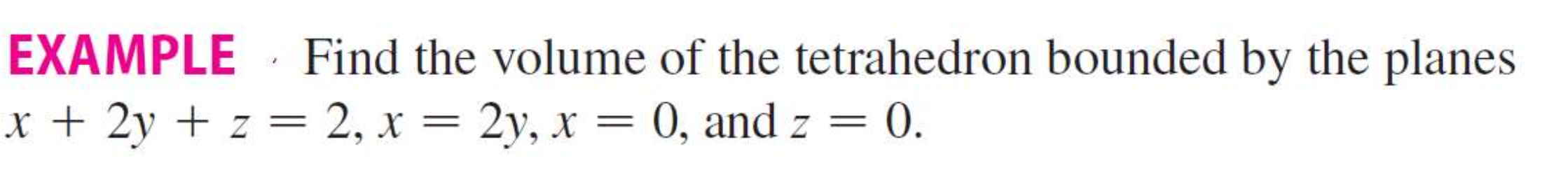
Understand the Problem
The question is asking us to find the volume of a tetrahedron defined by specific planes. We will determine the points of intersection and calculate the volume based on the geometry of the shape defined by the given equations.
Answer
The volume of the tetrahedron is \(V = \frac{1}{3}\).
Answer for screen readers
The volume of the tetrahedron is (V = \frac{1}{3}).
Steps to Solve
-
Identify the planes and their equations
The planes bounding the tetrahedron are:- Plane 1: $x + 2y + z = 2$
- Plane 2: $x = 2y$
- Plane 3: $x = 0$ (the yz-plane)
- Plane 4: $z = 0$ (the xy-plane)
-
Find the intersection points of the planes
We need to find the vertices of the tetrahedron by finding the intersection of the planes.-
Intersection of $x + 2y + z = 2$ and $x = 0$: [ 0 + 2y + z = 2 \implies z = 2 - 2y ]
For $y = 0$, we get the point $(0, 0, 2)$. -
Intersection of $x + 2y + z = 2$ and $x = 2y$: [ 2y + 2y + z = 2 \implies 4y + z = 2 \implies z = 2 - 4y ] If $y = 0$, we find the point $(0, 0, 2)$. For $y = 0.5$, we find the point $(1, 0.5, 0)$.
-
Intersection of $x = 2y$, $z = 0$, and $x = 0$: This yields the point $(0, 0, 0)$.
-
Intersection of $x = 0$, $z = 0$, and $y = 1$: Yields point $(0, 1, 0)$.
-
After solving, the vertices are:
- $A(0, 0, 2)$
- $B(0, 1, 0)$
- $C(1, 0.5, 0)$
- $D(0, 0, 0)$
-
Calculate the volume using the vertices
The volume $V$ of a tetrahedron with vertices at $(x_1, y_1, z_1)$, $(x_2, y_2, z_2)$, $(x_3, y_3, z_3)$, and $(x_4, y_4, z_4)$ is given by the formula:
[ V = \frac{1}{6} \left| \begin{vmatrix} x_1 & y_1 & z_1 & 1 \ x_2 & y_2 & z_2 & 1 \ x_3 & y_3 & z_3 & 1 \ x_4 & y_4 & z_4 & 1 \end{vmatrix} \right| ]
Using points (A(0, 0, 2)), (B(0, 1, 0)), (C(1, 0.5, 0)), and (D(0, 0, 0)):
[
V = \frac{1}{6} \left| \begin{vmatrix}
0 & 0 & 2 & 1 \
0 & 1 & 0 & 1 \
1 & 0.5 & 0 & 1 \
0 & 0 & 0 & 1
\end{vmatrix} \right|
]
-
Evaluate the determinant
Calculating the determinant, we find:
[ = \left| 0\cdot(1 \cdot 0 - 0.5 \cdot 0) - 0\cdot(0 \cdot 0 - 0 \cdot 1) + 2\cdot(0 \cdot 1 - 0\cdot 0) - 1\cdot(0 \cdot 0.5 - 1\cdot 0) \right| = -2 ]
So,
[ V = \frac{1}{6} \cdot 2 = \frac{1}{3} ]
The volume of the tetrahedron is (V = \frac{1}{3}).
More Information
Tetrahedrons are a type of polyhedron that have four faces. The volume formula used here derives from linear algebra concepts involving determinants.
Tips
- Failing to find all intersection points correctly, leading to wrong vertices.
- Miscalculating the determinant, which is crucial for finding the final volume.
- Not considering that volume must be positive, so always take the absolute value.
AI-generated content may contain errors. Please verify critical information