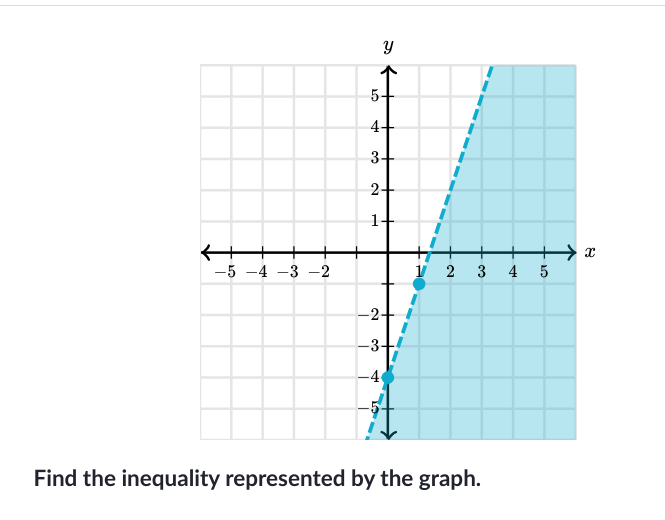
Find the inequality represented by the graph.

Understand the Problem

The question is asking to identify the inequality that corresponds to the graph provided. The graph shows a boundary line and a shaded area, indicating the region that satisfies the inequality.

Answer

The inequality is $y < \frac{5}{2}x - 5$.

Steps to Solve

Identify the boundary line The graph shows a dashed boundary line. A dashed line indicates that the points on the line are not included in the solution, meaning we will use a strict inequality (either $<$ or $>$).
Determine the equation of the boundary line From the graph, we can select two points on the line to determine its equation. The line passes through (2, 5) and has a slope indicating a rise/run of 1/1. The slope (m) is calculated by finding the change in $y$ and $x$ between two points.
Write the equation in slope-intercept form Using the slope-intercept form $y = mx + b$, where $m$ is the slope and $b$ is the y-intercept: [ b = 5 \quad (\text{y-intercept from the graph}) ] Calculating the slope from the points: [ m = \frac{5 - 0}{2 - 0} = \frac{5}{2} ] Thus, the equation is $y = \frac{5}{2}x - 5$.
Analyze the shaded region The shaded region is above the boundary line, indicating that $y$ is greater than the line. Therefore, the inequality takes the form: [ y < \frac{5}{2}x - 5 ] Since the line is dashed, it confirms the strict inequality.

The inequality represented by the graph is $$ y < \frac{5}{2}x - 5 $$.

More Information

This inequality describes a region where all values of $y$ are less than the value given by the boundary line $y = \frac{5}{2}x - 5$. The graph representation helps visualize the solution set.

Tips

Misidentifying the type of line (dashed vs solid). Solid lines indicate "≤" or "≥", while dashed lines indicate "<" or ">".
Incorrectly calculating the slope or y-intercept from the graph.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!