Find the volume of the solid generated by revolving the region between the y-axis and the curve x = 2/y, 1 ≤ y ≤ 4, about the y-axis.
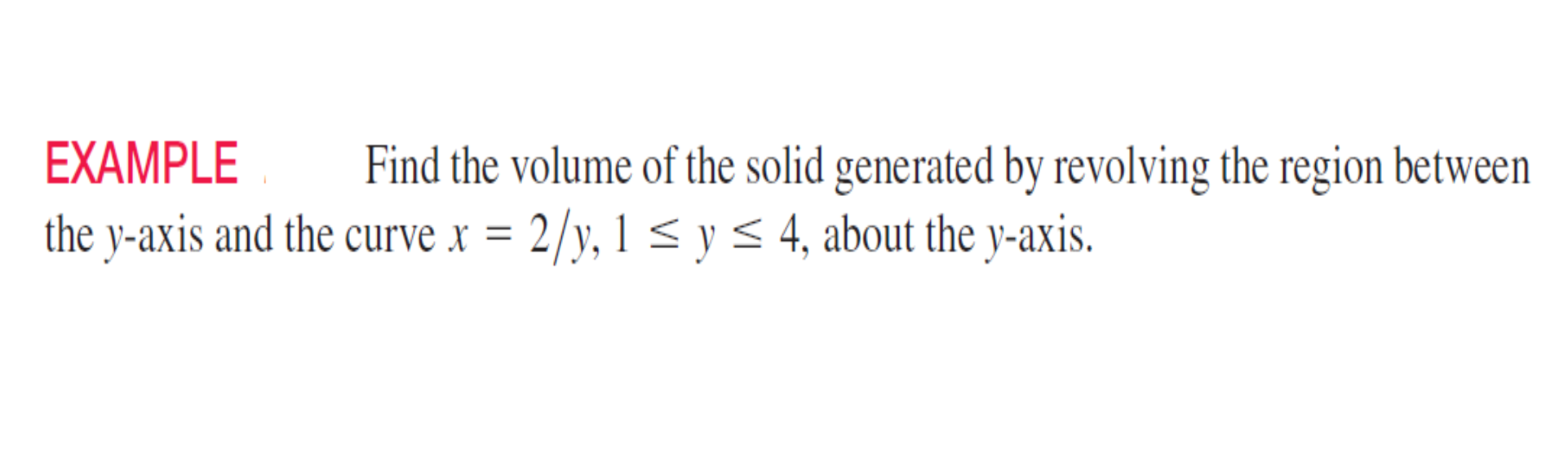
Understand the Problem
The question is asking for the calculation of the volume of a solid formed by revolving a specific region around the y-axis. This involves integral calculus, particularly the method of washers or disks.
Answer
The volume of the solid is \( V = 3\pi \).
Answer for screen readers
The volume of the solid generated is ( V = 3\pi ).
Steps to Solve
- Identify the region and function
The curve is given by the equation $x = \frac{2}{y}$. We need to consider the region bounded by this curve and the y-axis for $1 \leq y \leq 4$.
- Set up the volume integral
To find the volume of the solid formed by revolving this region around the y-axis, we use the formula:
$$ V = \pi \int_{a}^{b} [R(y)]^2 , dy $$
where $R(y)$ is the distance from the y-axis to the curve.
- Determine the function for $R(y)$
From the equation $x = \frac{2}{y}$, the radius function $R(y)$ is equal to $\frac{2}{y}$. Thus, we have:
$$ R(y) = \frac{2}{y} $$
- Calculate the volume integral
Substituting our limits ($a = 1$ and $b = 4$) and the function into the volume formula, the integral becomes:
$$ V = \pi \int_{1}^{4} \left(\frac{2}{y}\right)^2 , dy $$
- Evaluate the integral
We need to simplify the square and evaluate:
$$ \left(\frac{2}{y}\right)^2 = \frac{4}{y^2} $$
Thus,
$$ V = \pi \int_{1}^{4} \frac{4}{y^2} , dy $$
Now, calculating the integral:
$$ V = \pi \left[ -\frac{4}{y} \right]_{1}^{4} $$
Substituting the limits:
$$ V = \pi \left( -\frac{4}{4} + \frac{4}{1} \right) = \pi \left( -1 + 4 \right) = 3\pi $$
The volume of the solid generated is ( V = 3\pi ).
More Information
This result shows how the method of shells (or washers) can be employed in calculus to find volumes of solids of revolution. The shape formed in this case rotates around the y-axis, demonstrating the use of integral calculus in a practical application.
Tips
Some common mistakes include:
- Misidentifying the boundaries of integration. Ensure the limits $y = 1$ and $y = 4$ are correct.
- Incorrectly setting up the radius function $R(y)$. It must represent the distance from the y-axis.
- Failing to simplify the integral before calculating.
AI-generated content may contain errors. Please verify critical information