Evaluate \( \int_0^1 \int_0^x (x+y) \, dy \, dx \)
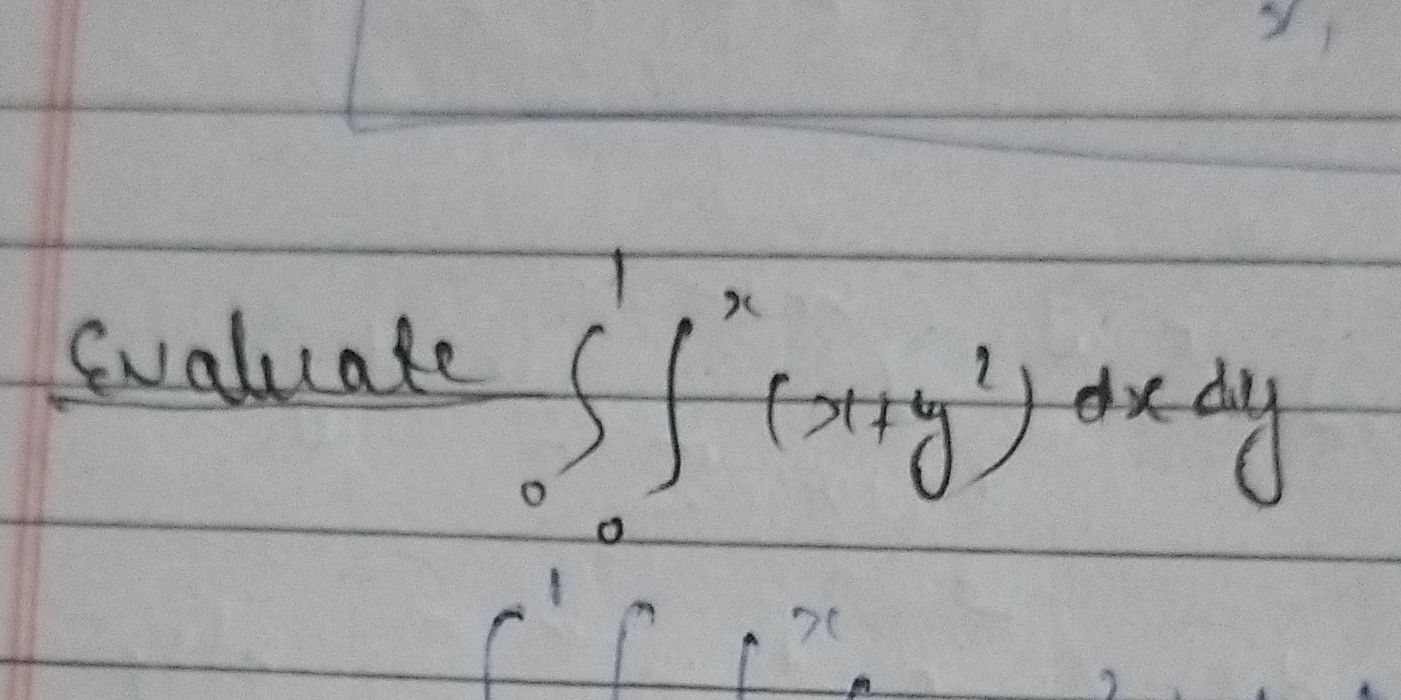
Understand the Problem
The question is asking to evaluate a double integral of the function (x+y) over a specific range defined by the limits of integration. It involves understanding integration techniques and potentially iterated integrals.
Answer
The integral evaluates to \( \frac{1}{2} \).
Answer for screen readers
The final answer is ( \frac{1}{2} ).
Steps to Solve
- Evaluate the inner integral
Begin by evaluating the inner integral with respect to (y):
$$ \int_0^x (x + y) , dy $$
Split the integral into two parts:
$$ \int_0^x x , dy + \int_0^x y , dy $$
The first part is:
$$ \int_0^x x , dy = x \cdot y \bigg|_0^x = x^2 $$
And the second part is:
$$ \int_0^x y , dy = \frac{y^2}{2} \bigg|_0^x = \frac{x^2}{2} $$
Combine both results:
$$ \int_0^x (x + y) , dy = x^2 + \frac{x^2}{2} = \frac{3x^2}{2} $$
- Evaluate the outer integral
Now evaluate the outer integral:
$$ \int_0^1 \frac{3x^2}{2} , dx $$
Factor out the constant:
$$ \frac{3}{2} \int_0^1 x^2 , dx $$
Now, compute the integral:
$$ \int_0^1 x^2 , dx = \frac{x^3}{3} \bigg|_0^1 = \frac{1}{3} $$
Combine with the constant:
$$ \frac{3}{2} \cdot \frac{1}{3} = \frac{1}{2} $$
- Final answer
The value of the double integral is:
$$ \int_0^1 \int_0^x (x+y) , dy , dx = \frac{1}{2} $$
The final answer is ( \frac{1}{2} ).
More Information
This integral demonstrates the use of iterated integrals and shows how to handle integrals of polynomial functions, a common technique in calculus.
Tips
- Forgetting to evaluate limits correctly: Always remember to apply the limits after integrating.
- Mistaking variable substitutions: Ensure each variable's limits are consistent with the order of integration.
AI-generated content may contain errors. Please verify critical information