Find the volume of the prism whose base is the triangle in the xy-plane bounded by the x-axis and the lines y = x and x = 1 and whose top lies in the plane z = f(x, y) = 3 - x - y.
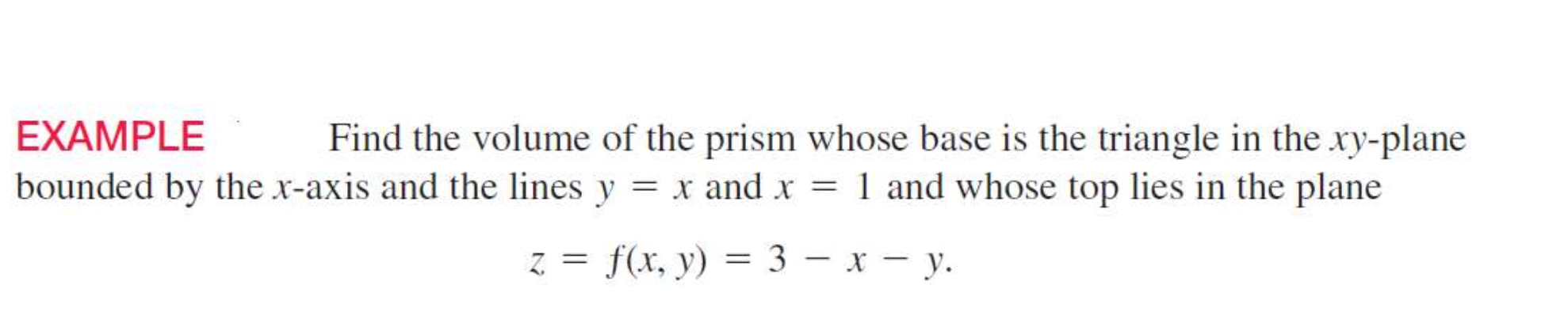
Understand the Problem
The question is asking to find the volume of a prism based on a triangular base in the xy-plane, with specific constraints provided for the boundaries and a given function for the height. We will need to analyze the region defined by the x-axis, the lines y = x, and x = 1, and then apply the appropriate integration techniques to compute the volume.
Answer
$V = 1$ cubic unit.
Answer for screen readers
The volume of the prism is $V = 1$ cubic unit.
Steps to Solve
-
Define the region of integration
The triangular region in the xy-plane is defined by the x-axis, the line $y = x$, and the vertical line $x = 1$. The vertices of the triangle are at the points $(0, 0)$, $(1, 0)$, and $(1, 1)$.
-
Set up the double integral
To find the volume of the prism, we need to set up a double integral over the triangular region with the integrand being the height function $z = f(x, y) = 3 - x - y$. The volume $V$ can be expressed as: $$ V = \int_{0}^{1} \int_{0}^{x} (3 - x - y) , dy , dx $$
-
Evaluate the inner integral
First, we will evaluate the inner integral with respect to $y$: $$ \int_{0}^{x} (3 - x - y) , dy $$ This becomes: $$ = \left[ (3 - x)y - \frac{y^2}{2} \right]_{0}^{x} = (3 - x)x - \frac{x^2}{2} $$ Simplifying this expression gives us: $$ = 3x - x^2 - \frac{x^2}{2} = 3x - \frac{3}{2} x^2 $$
-
Evaluate the outer integral
Now we substitute the result of the inner integral into the outer integral: $$ V = \int_{0}^{1} \left( 3x - \frac{3}{2} x^2 \right) , dx $$ This can be evaluated as: $$ = \left[ \frac{3}{2} x^2 - \frac{3}{6} x^3 \right]_{0}^{1} = \left( \frac{3}{2} \cdot 1^2 - \frac{3}{6} \cdot 1^3 \right) - 0 $$ Simplifying yields: $$ = \frac{3}{2} - \frac{1}{2} = 1 $$
-
Final volume result
Thus, the volume of the prism is $V = 1$ cubic unit.
The volume of the prism is $V = 1$ cubic unit.
More Information
This problem involves calculating the volume under a surface defined by a height function over a triangular region in the xy-plane. The approach involves setting up double integrals and carefully evaluating them.
Tips
- Forgetting to correctly identify the limits of integration for either variable.
- Failing to simplify the integrals properly, resulting in incorrect final answers.
- Not keeping track of the boundaries of the region while setting up the double integral.
AI-generated content may contain errors. Please verify critical information