Find the values of x if p + 7 = 0, q - 12 = 0 and x^2 + px + q = 0. If x = p is a solution of the equation x(2x + 5) = 3, then find the values of p. If x = 3 is a solution of the e... Find the values of x if p + 7 = 0, q - 12 = 0 and x^2 + px + q = 0. If x = p is a solution of the equation x(2x + 5) = 3, then find the values of p. If x = 3 is a solution of the equation (k + 2)x^2 - kx + 6 = 0, find the value of k. Hence, find the other root of the equation.
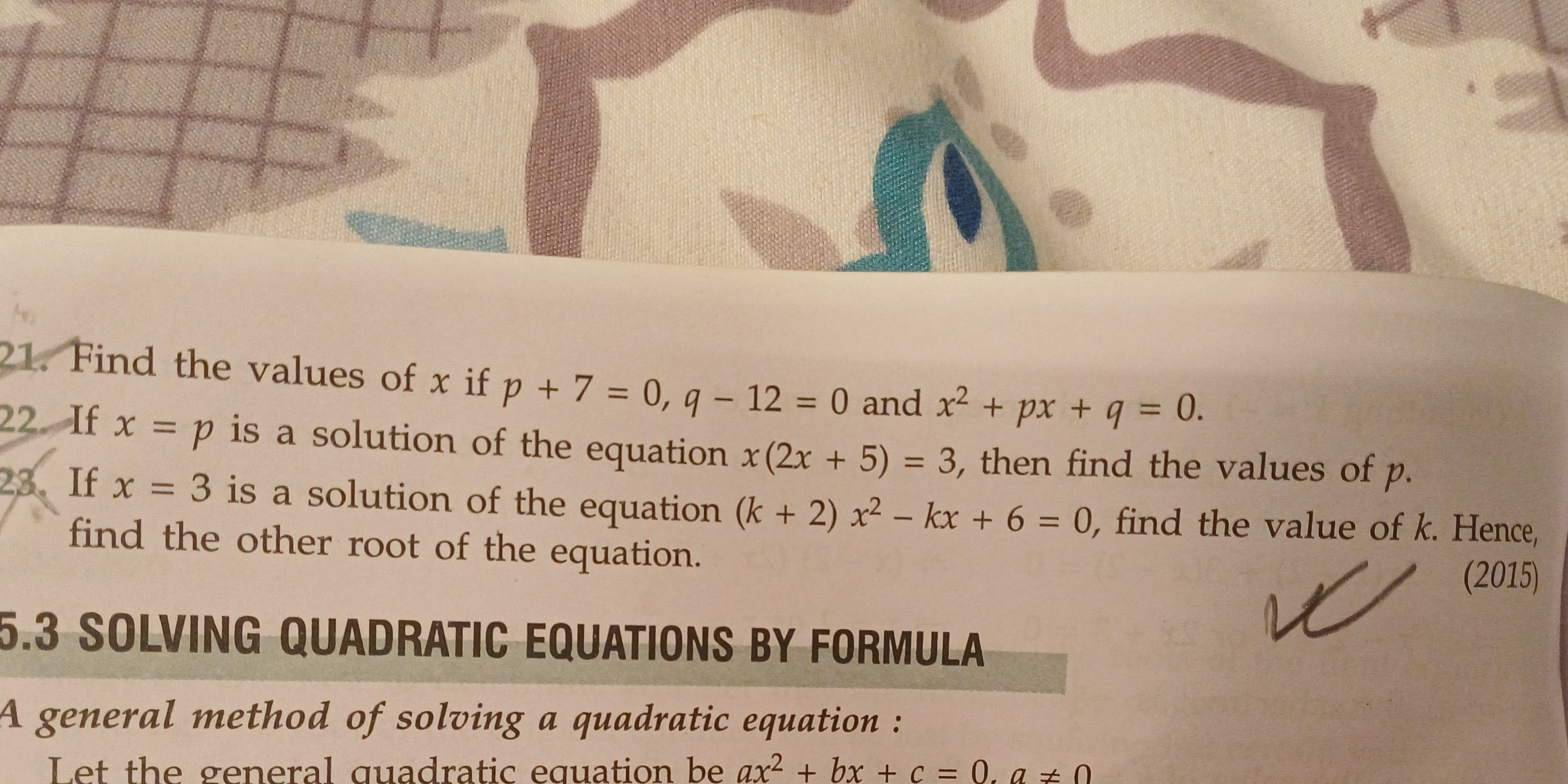
Understand the Problem
The question is asking to find the values of variables within a set of equations related to solving quadratic equations. It involves finding the values of x for certain conditions and determining specific parameters in quadratic equations.
Answer
$p = -7$, $q = 12$, $k = -4$, other root = $-1$.
Answer for screen readers
The values are ( p = -7 ), ( q = 12 ), and ( k = -4 ). The other root of the equation is ( -1 ).
Steps to Solve
- Solve the first set of equations for ( p ) and ( q )
The equations given are ( p + 7 = 0 ) and ( q - 12 = 0 ).
To find ( p ) and ( q ):
-
From ( p + 7 = 0 ): $$ p = -7 $$
-
From ( q - 12 = 0 ): $$ q = 12 $$
- Substitute ( p ) into the equation ( x(2x + 5) = 3 )
We substitute ( p = -7 ) into the equation: $$ x(2x + 5) = 3 $$
Now expand and rearrange the equation: $$ 2x^2 + 5x - 3 = 0 $$
- Use the quadratic formula to find ( x )
The quadratic formula is given by: $$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
For the equation ( 2x^2 + 5x - 3 = 0 ):
- Coefficients are: ( a = 2 ), ( b = 5 ), ( c = -3 )
Plugging these into the quadratic formula: $$ x = \frac{-5 \pm \sqrt{5^2 - 4 \cdot 2 \cdot (-3)}}{2 \cdot 2} $$
Calculate the discriminant: $$ 5^2 - 4 \cdot 2 \cdot (-3) = 25 + 24 = 49 $$
So we have: $$ x = \frac{-5 \pm \sqrt{49}}{4} $$ $$ x = \frac{-5 \pm 7}{4} $$
Thus, the solutions are:
-
$$ x = \frac{2}{4} = \frac{1}{2} $$
-
$$ x = \frac{-12}{4} = -3 $$
-
Find the value of ( k ) using ( x = 3 ) in ( (k + 2)x^2 - kx + 6 = 0 )
Substituting ( x = 3 ) into ( (k + 2)(3^2) - k(3) + 6 = 0 ): $$ (k + 2)(9) - 3k + 6 = 0 $$ Expanding this gives: $$ 9k + 18 - 3k + 6 = 0 $$
Combining like terms: $$ 6k + 24 = 0 $$
Now solving for ( k ): $$ 6k = -24 $$ $$ k = -4 $$
- Calculate the other root of the quadratic equation
To find the other root, use the sum of the roots obtained from ( (k + 2)x^2 - kx + 6 = 0 ) with ( k = -4 ): $$ (k + 2) \text{ at } k = -4 $$ becomes ( -2x^2 + 4x + 6 = 0 ).
Using the sum of the roots:
- Let the roots be ( r_1 ) and ( r_2 ). We know ( r_1 + r_2 = -\frac{b}{a} = -\frac{4}{-2} = 2 ). Since ( r_1 = 3 ), we have: $$ 3 + r_2 = 2 $$ $$ r_2 = 2 - 3 = -1 $$
The values are ( p = -7 ), ( q = 12 ), and ( k = -4 ). The other root of the equation is ( -1 ).
More Information
These values illustrate how coefficients in quadratic equations can determine the roots. The process is commonly used in algebra to analyze polynomial behaviors.
Tips
- Forgetting to rearrange the equations before applying the quadratic formula.
- Not simplifying the expressions, leading to incorrect root values.
AI-generated content may contain errors. Please verify critical information