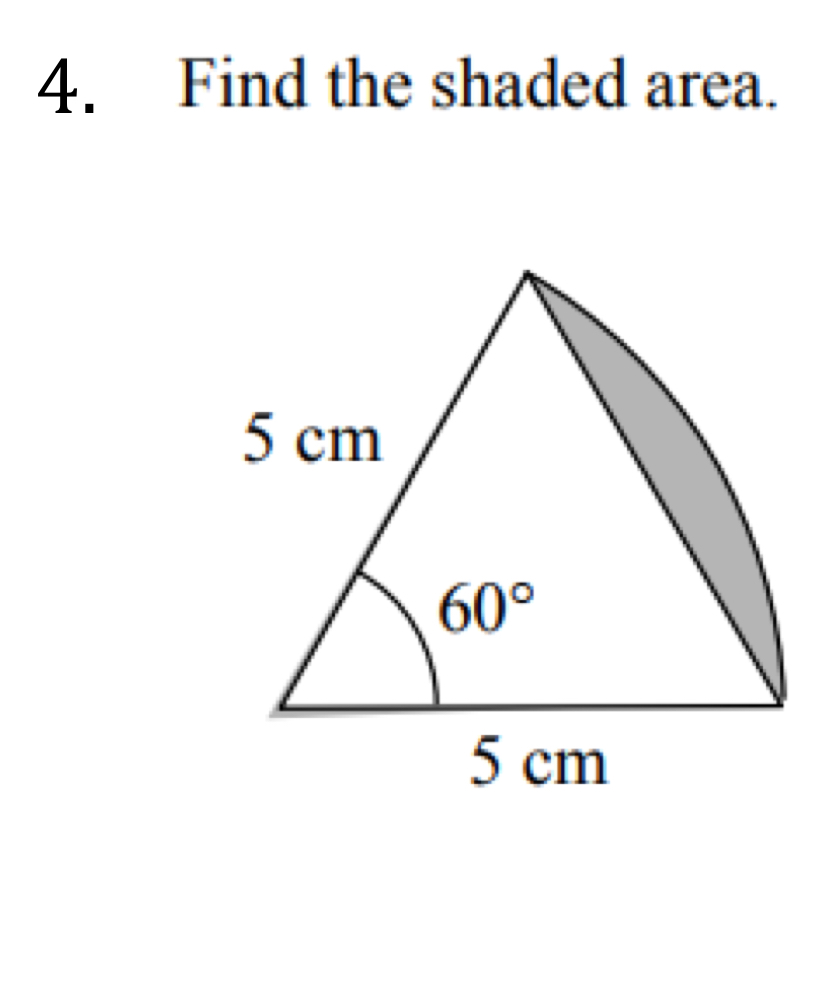
Find the shaded area.

Understand the Problem

The question is asking us to calculate the area of the shaded region in a triangle, where two sides measure 5 cm each and the included angle is 60 degrees. To find this area, we likely need to determine the area of the entire triangle and then subtract the area of the unshaded segment.

Answer

The area of the triangle is approximately $10.83 \, \text{cm}^2$.

Steps to Solve

Calculate the area of the triangle

To find the area of the triangle, we can use the formula: $$ \text{Area} = \frac{1}{2}ab \sin(C) $$ where ( a ) and ( b ) are the lengths of the sides, and ( C ) is the included angle. Here, ( a = 5 ) cm, ( b = 5 ) cm, and ( C = 60^\circ ).

Plugging in the values, we get: $$ \text{Area} = \frac{1}{2} \cdot 5 \cdot 5 \cdot \sin(60^\circ) $$

Calculate ( \sin(60^\circ) )

The sine of ( 60^\circ ) can be calculated as: $$ \sin(60^\circ) = \frac{\sqrt{3}}{2} $$

Now substituting this into the area formula: $$ \text{Area} = \frac{1}{2} \cdot 5 \cdot 5 \cdot \frac{\sqrt{3}}{2} = \frac{25\sqrt{3}}{4} $$

Calculate the numerical value of the area

To find a decimal approximation of the area: $$ \text{Area} \approx \frac{25 \cdot 1.732}{4} \approx 10.83 , \text{cm}^2 $$

Determine the unshaded section (if necessary)

If the problem asks for the unshaded area specifically, we will need to calculate the area of the segment or any corresponding part. For this particular problem, the focus is only on the triangle's area.

The area of the triangle is approximately $10.83 , \text{cm}^2$.

More Information

The area of a triangle can be effectively calculated using the sine of the included angle, which simplifies the computation when dealing with non-right triangles.

Tips

Forgetting to convert angles from degrees to radians when necessary for functions like sine (not applicable here).
Miscalculating ( \sin(60^\circ) ) as ( 0.5 ) instead of ( \frac{\sqrt{3}}{2} ).

AI-generated content may contain errors. Please verify critical information

Thank you for voting!