Find the scale factor. Show your work.

Understand the Problem

The question is asking to find the scale factor between two triangles given their dimensions. The scale factor can be calculated by comparing corresponding sides of the triangles.

Answer

The scale factor is $ 4 $.

Steps to Solve

Identify corresponding sides of the triangles

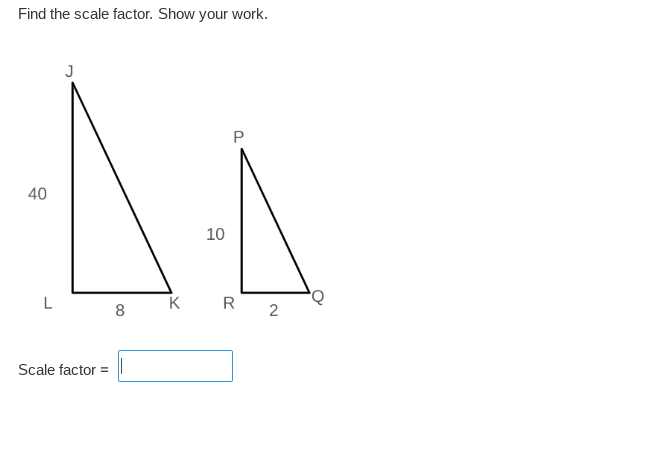
We have two triangles: Triangle JLK and Triangle PRQ. To find the scale factor, we need to compare the lengths of their corresponding sides.

For triangle JLK:
- Length J to L = 40
- Length L to K = 8
For triangle PRQ:
- Length P to R = 10
- Length R to Q = 2

Calculate the scale factor using corresponding sides

The scale factor can be calculated by dividing the length of a side in one triangle by the length of the corresponding side in the other triangle.

Using the height of the triangles: $$ \text{Scale factor} = \frac{\text{Length of J to L}}{\text{Length of P to R}} = \frac{40}{10} = 4 $$

Validate using the other set of corresponding sides

Next, we can check the scale factor using the base lengths:

$$ \text{Scale factor} = \frac{\text{Length of L to K}}{\text{Length of R to Q}} = \frac{8}{2} = 4 $$

Both calculations result in the same scale factor.

The scale factor is ( 4 ).

More Information

The scale factor indicates how many times larger one triangle is compared to the other. In this case, triangle JLK is 4 times larger than triangle PRQ.

Tips

Confusing which sides are corresponding can lead to incorrect calculations. Always double-check which sides relate to each other in similar figures.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!