¿Cuál de las siguientes acciones es la mejor para lanzar la pelota? A) Lanzar la pelota con un ángulo muy bajo; B) Lanzar la pelota a un ángulo de 45 grados; C) Lanzar la pelota lo... ¿Cuál de las siguientes acciones es la mejor para lanzar la pelota? A) Lanzar la pelota con un ángulo muy bajo; B) Lanzar la pelota a un ángulo de 45 grados; C) Lanzar la pelota lo más fuerte posible; D) Lanzar la pelota hacia el suelo. Con base en los datos anteriores, ¿cuál es la mediana de las distancias recorridas por la pelota?
Understand the Problem
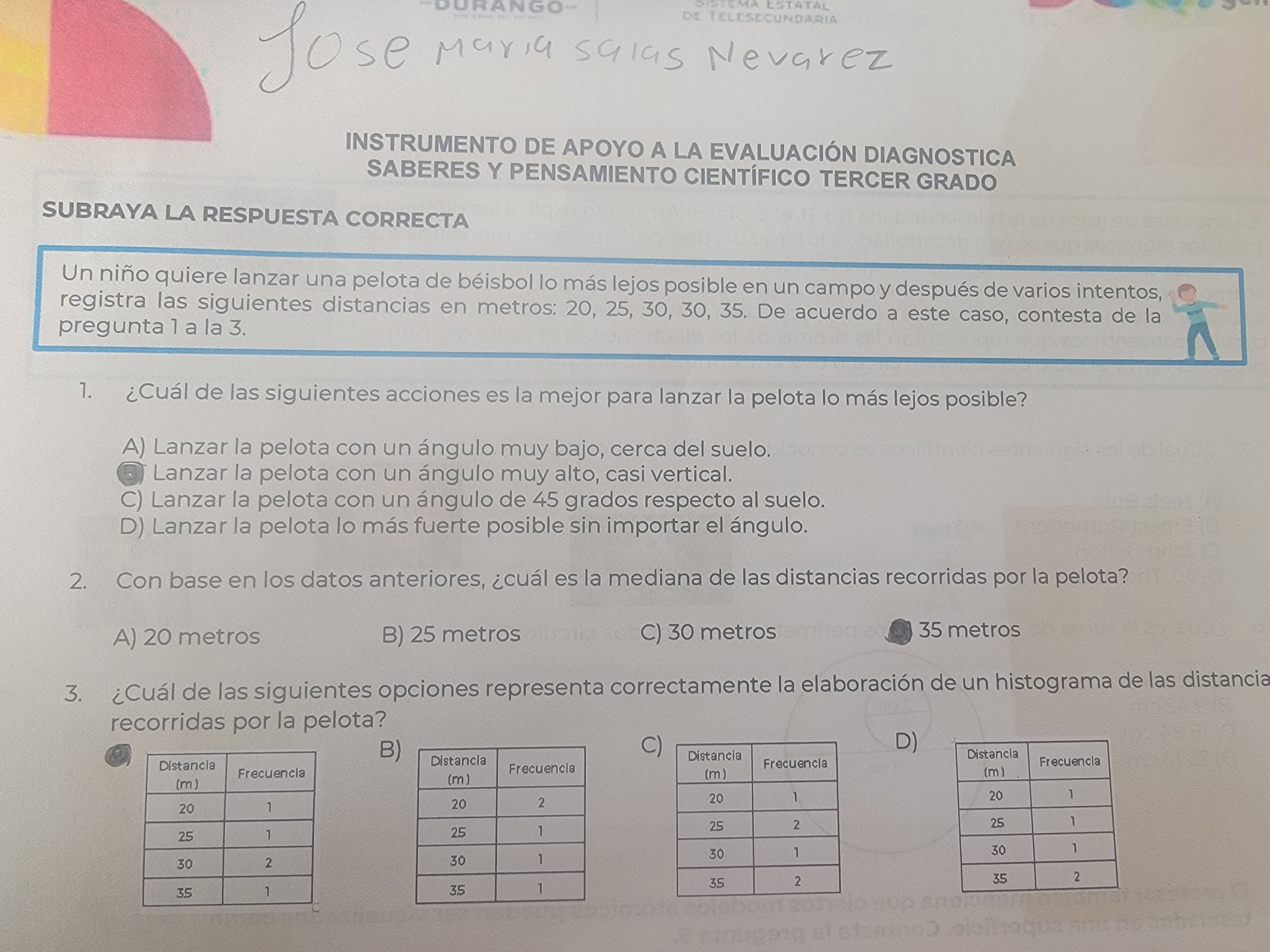
La pregunta se centra en determinar la mejor acción para lanzar una pelota para lograr la mayor distancia posible, así como calcular la mediana de las distancias recorridas según los datos proporcionados.
Answer
La mediana de las distancias recorridas por la pelota es $30$ metros.
Answer for screen readers
La mediana de las distancias recorridas por la pelota es 30 metros.
Steps to Solve
-
Lista de distancias recorridas Se nos dan las distancias en metros recorridas por la pelota: 20, 25, 30, 30, 35, 35.
-
Ordenar las distancias Primero, ordenamos las distancias de menor a mayor: 20, 25, 30, 30, 35, 35.
-
Encontrar la mediana La mediana se encuentra en el medio de un conjunto de datos ordenados. Si hay un número impar de datos, es el valor del medio; si es par, se promedian los dos valores del medio.
Aquí tenemos 6 datos (un número par):
- Los dos números del medio son 30 y 30.
- Calcular la mediana La mediana se calcula promediando los dos números del medio:
$$ \text{Mediana} = \frac{30 + 30}{2} = 30 $$
La mediana de las distancias recorridas por la pelota es 30 metros.
More Information
La mediana es un dato estadístico que representa el valor central de un conjunto de datos ordenados. En contextos como este, la mediana puede ser útil para comprender cuál es la distancia típica alcanzada por la pelota sin verse afectada por valores extremos.
Tips
- Confundir la media con la mediana: La media es el promedio de todos los valores, mientras que la mediana es el valor central. Asegúrate de entender la diferencia.
- No ordenar los datos: Es esencial ordenar las distancias antes de calcular la mediana.
AI-generated content may contain errors. Please verify critical information