Find the quadratic equation with the roots (α², β³) = 3 and α - β = 2.
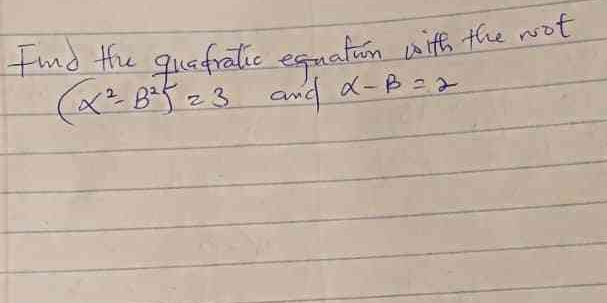
Understand the Problem
The question is asking to find a quadratic equation given specific roots and a condition relating the roots. This involves applying knowledge of quadratic equations and their properties, such as the relationships between roots and coefficients.
Answer
The quadratic equation can be expressed after solving: $$x^2 - (r+s)x + rs = 0$$ where \(r\) and \(s\) are determined from \(s^5 + 4s^4 + 4s^3 - 3 = 0\).
Answer for screen readers
The roots of the quadratic equation can be found from:
$$s^5 + 4s^4 + 4s^3 - 3 = 0$$
After determining the values for (r) and (s) from this polynomial, we would then construct the quadratic equation.
Steps to Solve
- Substituting Variables for Roots
Let ( \alpha = r ) and ( \beta = s ) for easier notation. We know that:
$$(r^2)(s^3) = 3$$
and
$$r - s = 2$$
- Express ( r ) in Terms of ( s )
From the equation ( r - s = 2 ), we can express ( r ) as:
$$r = s + 2$$
- Substituting ( r ) into the Product Equation
Substitute the expression for ( r ) into the product equation:
$$(s + 2)^2 (s^3) = 3$$
- Expand and Simplify
Expanding ( (s + 2)^2 ):
$$(s^2 + 4s + 4)(s^3) = 3$$
This gives us:
$$s^5 + 4s^4 + 4s^3 = 3$$
- Rearranging the Equation
Rearranging to form a standard polynomial:
$$s^5 + 4s^4 + 4s^3 - 3 = 0$$
- Finding the Quadratic Equation
To find the quadratic equation, we can start with Vieta's formulas. For a quadratic equation of the form (x^2 - (r+s)x + rs = 0), we need the values of (r+s) and (rs).
From the previous steps, we can also determine (r) and (s) (the roots) once we solve the polynomial.
The roots of the quadratic equation can be found from:
$$s^5 + 4s^4 + 4s^3 - 3 = 0$$
After determining the values for (r) and (s) from this polynomial, we would then construct the quadratic equation.
More Information
The roots (r) and (s) derived from the polynomial will allow for the formation of the quadratic equation. Vieta's formulas will help relate the coefficients to the roots.
Tips
- Assuming incorrect forms of the quadratic without checking relationships between roots.
- Failing to properly expand or rearrange polynomials can lead to incorrect conclusions.
AI-generated content may contain errors. Please verify critical information