(2√3 + 3)(√3 + 5).

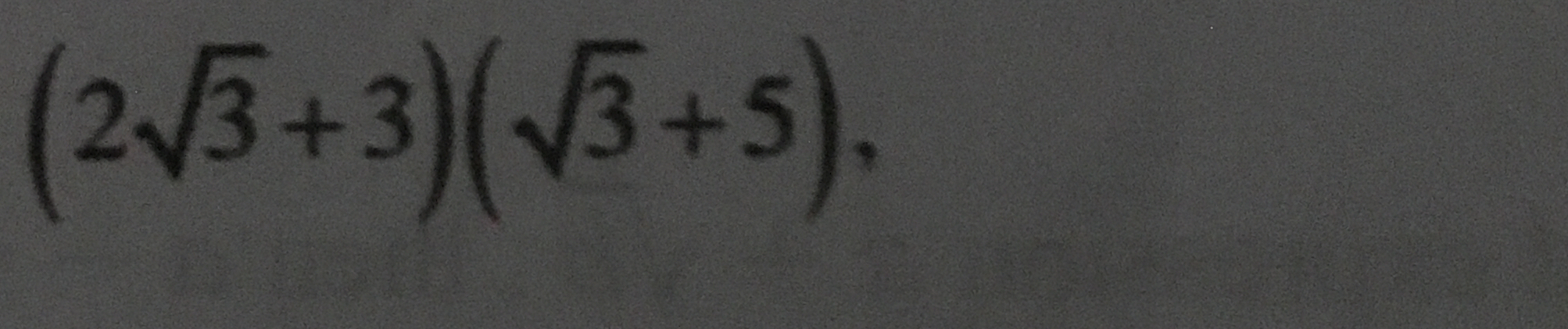
Understand the Problem

The question presents a mathematical expression involving square roots and requires simplification or calculation of the expression (2√3 + 3)(√3 + 5).

Answer

The simplified expression is $ 21 + 13\sqrt{3} $.

Steps to Solve

Expand the expression using the distributive property

We will use the distributive property (also known as the FOIL method for two binomials) to expand the expression:

$$(2\sqrt{3} + 3)(\sqrt{3} + 5)$$

Multiply the terms

Apply the FOIL method:

First: Multiply the first terms: $$ 2\sqrt{3} \cdot \sqrt{3} = 2 \cdot 3 = 6 $$
Outer: Multiply the outer terms: $$ 2\sqrt{3} \cdot 5 = 10\sqrt{3} $$
Inner: Multiply the inner terms: $$ 3 \cdot \sqrt{3} = 3\sqrt{3} $$
Last: Multiply the last terms: $$ 3 \cdot 5 = 15 $$

Combine like terms

Now we combine all the products we computed:

$$ 6 + 10\sqrt{3} + 3\sqrt{3} + 15 $$

Combine the like terms ($10\sqrt{3}$ and $3\sqrt{3}$):

$$ 6 + 15 + (10\sqrt{3} + 3\sqrt{3}) = 21 + 13\sqrt{3} $$

The simplified expression is ( 21 + 13\sqrt{3} ).

More Information

The final expression consists of a rational part and an irrational part. The number ( \sqrt{3} ) is approximately 1.732, thus ( 13\sqrt{3} ) is about 22.576, making the entire expression roughly ( 43.576 ).

Tips

Forgetting to combine like terms after multiplying.
Misapplying the distributive property and missing a term.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!