Find the quadratic equation with the roots (α² − β²) = 3 and α − β = 2.
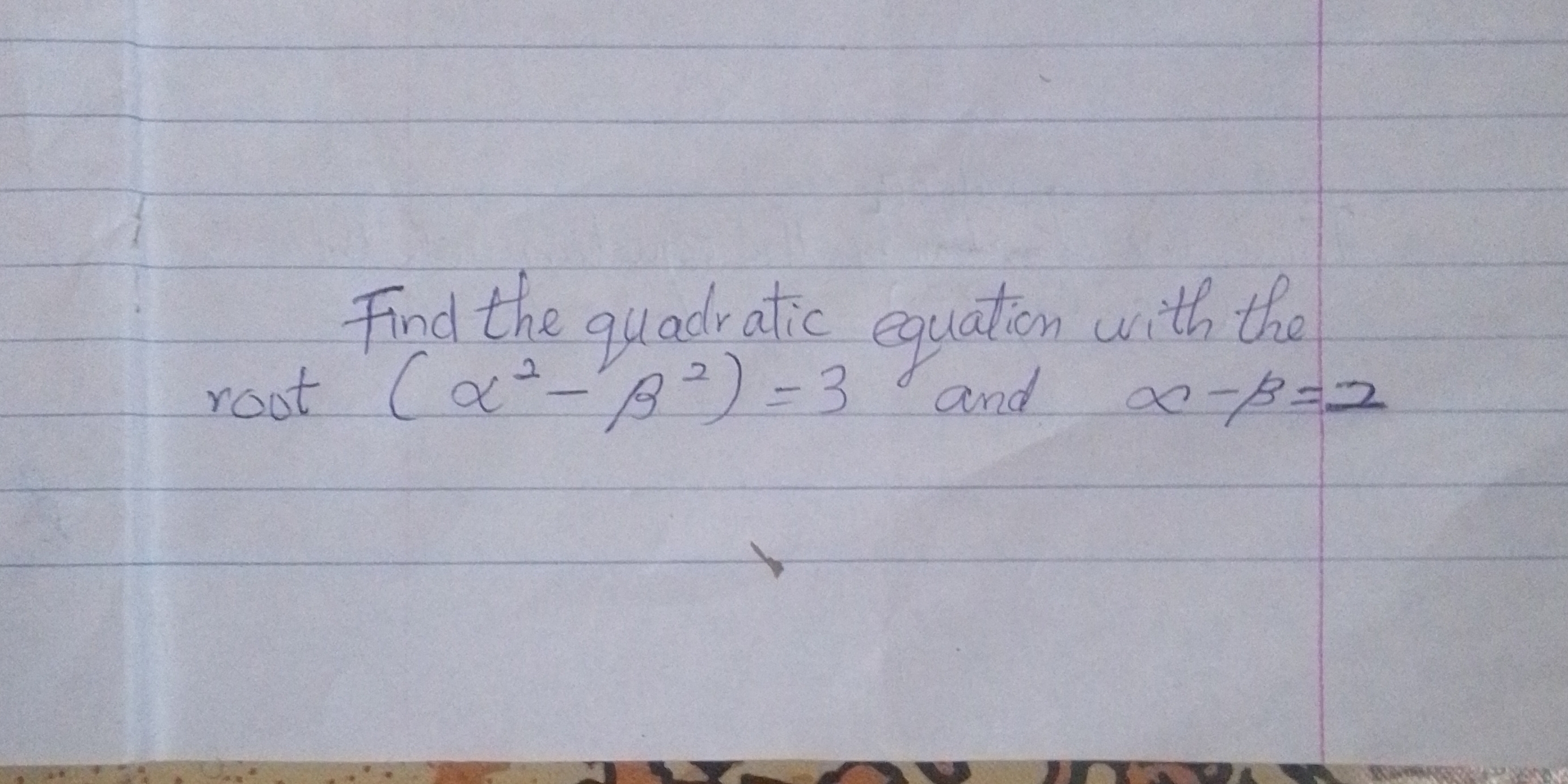
Understand the Problem
The question is asking to derive a quadratic equation based on the given roots and the conditions provided. We are given that the difference of the roots squared is equal to 3 and the difference of the roots is equal to 2. This leads to a series of algebraic manipulations to find the desired equation.
Answer
The quadratic equation is $x^2 - \frac{3}{2}x + p = 0$, where $p$ needs to be calculated from previous equations.
Answer for screen readers
The quadratic equation is given by: $$x^2 - \frac{3}{2}x + p = 0$$ Here, $p = \frac{1}{4}((\frac{3}{2})^2 - 2^2)$ must be calculated to provide the numeric value.
Steps to Solve
-
Using the difference of roots Given that $\alpha - \beta = 2$, we can square both sides to get: $$(\alpha - \beta)^2 = 2^2 = 4$$
-
Using the difference of squares equation We know that $\alpha^2 - \beta^2 = (\alpha - \beta)(\alpha + \beta)$. Therefore, we can rewrite the given condition: $$\alpha^2 - \beta^2 = 3$$ Substituting $\alpha - \beta = 2$ into the equation gives: $$3 = 2(\alpha + \beta)$$
-
Solving for the sum of the roots From the equation $3 = 2(\alpha + \beta)$, we can isolate $\alpha + \beta$: $$\alpha + \beta = \frac{3}{2}$$
-
Formulating the quadratic equation Now we have both the sum and the difference of the roots. The standard form of a quadratic equation is given by: $$x^2 - sx + p = 0$$ where $s = \alpha + \beta$ and $p = \alpha \beta$. To find $p$, we can use: $$\alpha^2 - \beta^2 = 3 \implies (\alpha - \beta)(\alpha + \beta) = 3$$
-
Finding the value of $\alpha \beta$ Using $\alpha + \beta = \frac{3}{2}$ and $\alpha - \beta = 2$, we already have: $$(2)(\frac{3}{2}) = 3$$ Now, applying the quadratic formula: We can derive by substituting both values into $p = \frac{1}{4}((\alpha + \beta)^2 - (\alpha - \beta)^2) = \frac{1}{4}((\frac{3}{2})^2 - 2^2)$.
-
Combining results Once we calculate $\alpha \beta$, we can substitute $s$ and $p$ into the standard form to create the quadratic equation.
The quadratic equation is given by: $$x^2 - \frac{3}{2}x + p = 0$$ Here, $p = \frac{1}{4}((\frac{3}{2})^2 - 2^2)$ must be calculated to provide the numeric value.
More Information
In this case, the roots and the resultant quadratic equation provide insight into relationships between the roots in quadratic functions, which is useful in various mathematical applications.
Tips
- Misinterpreting the difference of squares and roots could lead to incorrect calculations when setting up the equations.
- Forgetting to square the difference of roots properly can result in an incorrect sum or product of roots.
AI-generated content may contain errors. Please verify critical information