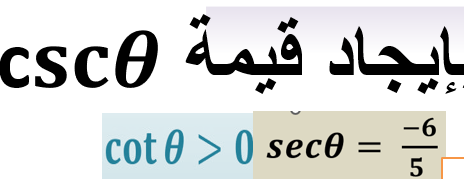
إيجاد قيمة cscθ إذا كانت cotθ > 0 و secθ = -6/5.

Steps to Solve

1. فهم الشروط المحيطة بالزاوية
   بما أن $secθ = -\frac{6}{5}$، فهذا يعني أن $cosθ = -\frac{5}{6}$.
   وبما أن $cotθ > 0$، فإنه من الضروري أن تكون $sinθ$ و$cosθ$ في نفس الربع، مما يعني أن $θ$ يجب أن يكون في الربع الثالث.

2. حساب قيمة $sinθ$ باستخدام هوية Pythagorean
   تستخدم الهوية $sin^2θ + cos^2θ = 1$.
   ليكن $cosθ = -\frac{5}{6}$، إذن:

$$ sin^2θ = 1 - \left(-\frac{5}{6}\right)^2 = 1 - \frac{25}{36} = \frac{36}{36} - \frac{25}{36} = \frac{11}{36} $$

وبالتالي، $sinθ = -\sqrt{\frac{11}{36}} = -\frac{\sqrt{11}}{6}$ (لأن $θ$ في الربع الثالث، يكون $sinθ$ سالب).

3. حساب قيمة $cscθ$
   بما أن $cscθ = \frac{1}{sinθ}$، فإن:

$$ cscθ = \frac{1}{-\frac{\sqrt{11}}{6}} = -\frac{6}{\sqrt{11}} $$

وبت rationalizing the denominator:

$$ cscθ = -\frac{6\sqrt{11}}{11} $$