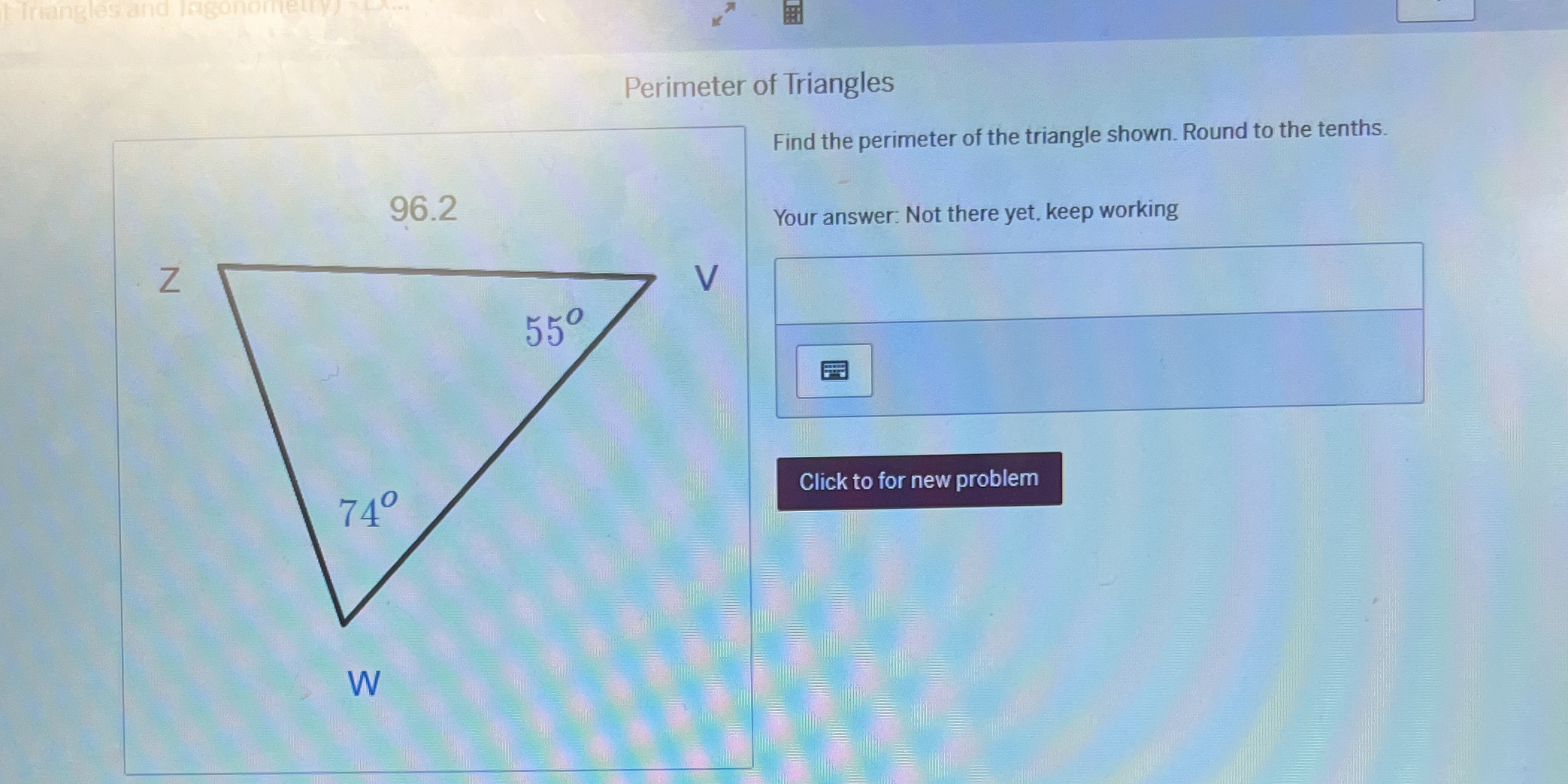
Find the perimeter of the triangle shown. Round to the tents.

Steps to Solve

1. Understand the triangle's properties

The triangle has one side (length $ZW = 96.2$) and two angles ($\angle W = 74^\circ$ and $\angle V = 55^\circ$). First, we need to find the third angle, $\angle Z$.

Using the triangle angle sum property: $$ \angle Z = 180^\circ - \angle W - \angle V $$

2. Calculate the value of angle Z

Substituting the known angle values: $$ \angle Z = 180^\circ - 74^\circ - 55^\circ $$ This gives us: $$ \angle Z = 180^\circ - 129^\circ = 51^\circ $$

3. Apply the Law of Sines

We can use the Law of Sines to find the lengths of the sides $ZW$ and $WV$: $$ \frac{ZW}{\sin Z} = \frac{WV}{\sin W} = \frac{VW}{\sin V} $$

We have: $$ \frac{96.2}{\sin(51^\circ)} = \frac{WV}{\sin(74^\circ)} $$

4. Find the length of side WV

Rearranging the equation, we solve for $WV$: $$ WV = \frac{96.2 \cdot \sin(74^\circ)}{\sin(51^\circ)} $$

5. Calculate the value for WV

Using a calculator:

• First, find $\sin(51^\circ) \approx 0.7771$ and $\sin(74^\circ) \approx 0.9613$.

Now calculate: $$ WV \approx \frac{96.2 \cdot 0.9613}{0.7771} \approx 120.7 $$

6. Find the length of side VW

Next, we calculate $VW$ using the Law of Sines: $$ \frac{96.2}{\sin(51^\circ)} = \frac{VW}{\sin(55^\circ)} $$

Rearranging gives: $$ VW = \frac{96.2 \cdot \sin(55^\circ)}{\sin(51^\circ)} $$

7. Calculate the value for VW

Using a calculator:

• Find $\sin(55^\circ) \approx 0.8192$.

Now calculate: $$ VW \approx \frac{96.2 \cdot 0.8192}{0.7771} \approx 101.1 $$

8. Calculate the perimeter of triangle ZWV

Finally, add up all the side lengths: $$ P = ZW + WV + VW $$ $$ P = 96.2 + 120.7 + 101.1 $$

9. Find the final perimeter

Calculating: $$ P \approx 318.0 $$