Find the other number x if HCF is 3 and LCM is 1170, with one number being 45.
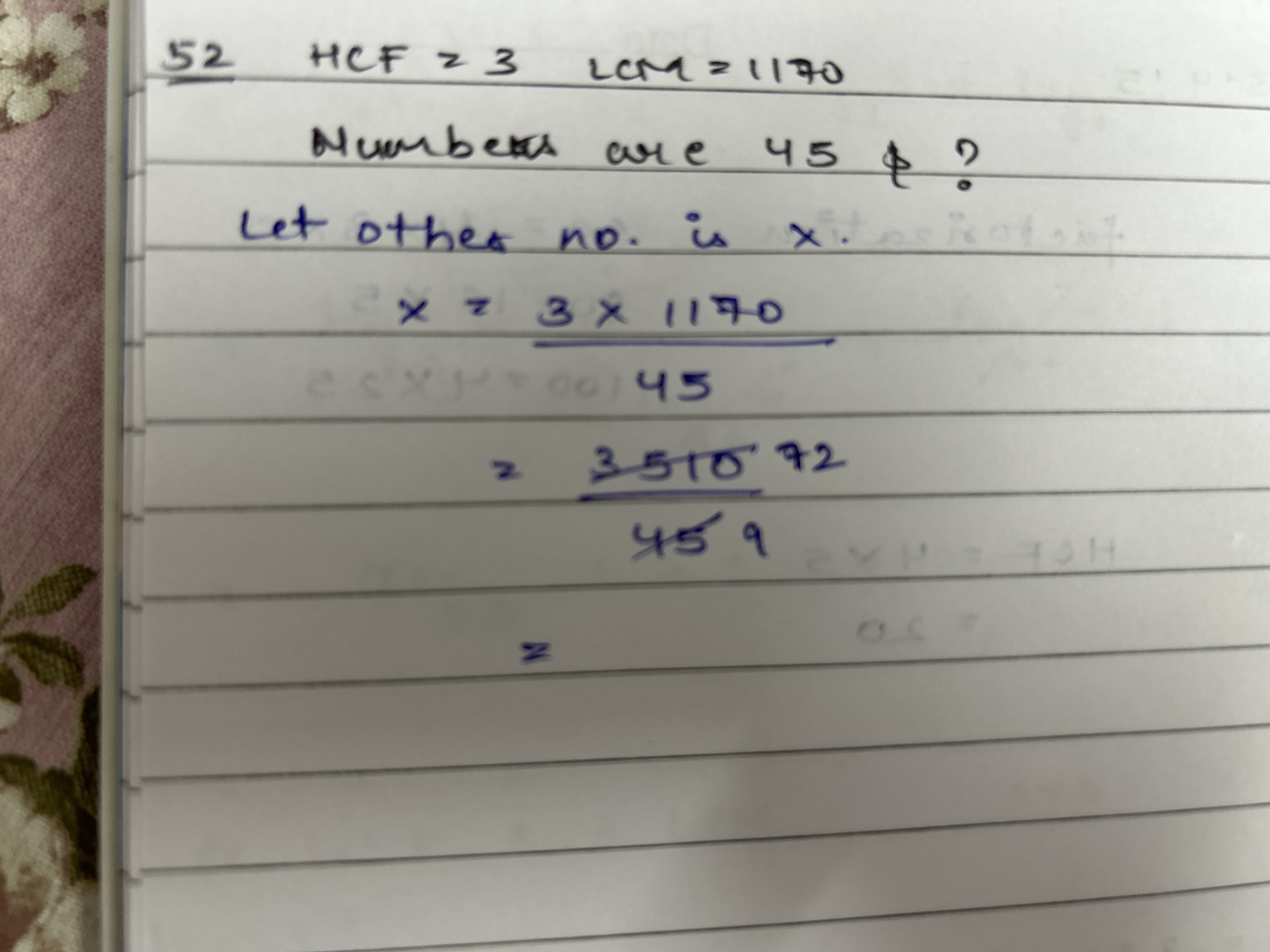
Understand the Problem
The question appears to be asking for a mathematical calculation involving the Highest Common Factor (HCF) and Lowest Common Multiple (LCM) of two numbers, which are 45 and 1170. The goal is to find the third number, denoted as x, based on these two given numbers.
Answer
The value of \( x \) is \( \frac{1}{15} \).
Answer for screen readers
The value of ( x ) is ( \frac{1}{15} ).
Steps to Solve
- Understanding HCF and LCM Relationship
The relationship between HCF (Highest Common Factor), LCM (Lowest Common Multiple), and the numbers involved is given by the formula: $$ \text{HCF} \times \text{LCM} = a \times b \times x $$ where ( a ) and ( b ) are the two known numbers, and ( x ) is the unknown number.
- Substituting Values
Substituting the known values into the formula:
- HCF = 3
- LCM = 1170
- Let ( a = 45 ) and ( b = 1170 ).
The equation becomes: $$ 3 \times 1170 = 45 \times 1170 \times x $$
- Calculating the Left Side
Now, calculate the left side: $$ 3 \times 1170 = 3510 $$
- Expressing the Right Side
Express the right side: $$ 45 \times 1170 = 52650 $$ So, we now have: $$ 3510 = 52650 \times x $$
- Solving for ( x )
To find ( x ), rearrange the equation: $$ x = \frac{3510}{52650} $$ Now simplify: $$ x = \frac{3510 \div 3510}{52650 \div 3510} = \frac{1}{15} $$
The value of ( x ) is ( \frac{1}{15} ).
More Information
This calculation shows that if you know the HCF and LCM of two numbers, you can easily find a third number using their product relation. This method is useful in various mathematical problems involving sets of numbers.
Tips
- Confusing LCM with HCF; remember they are different concepts.
- Forgetting to simplify the fraction when calculating ( x ).
AI-generated content may contain errors. Please verify critical information