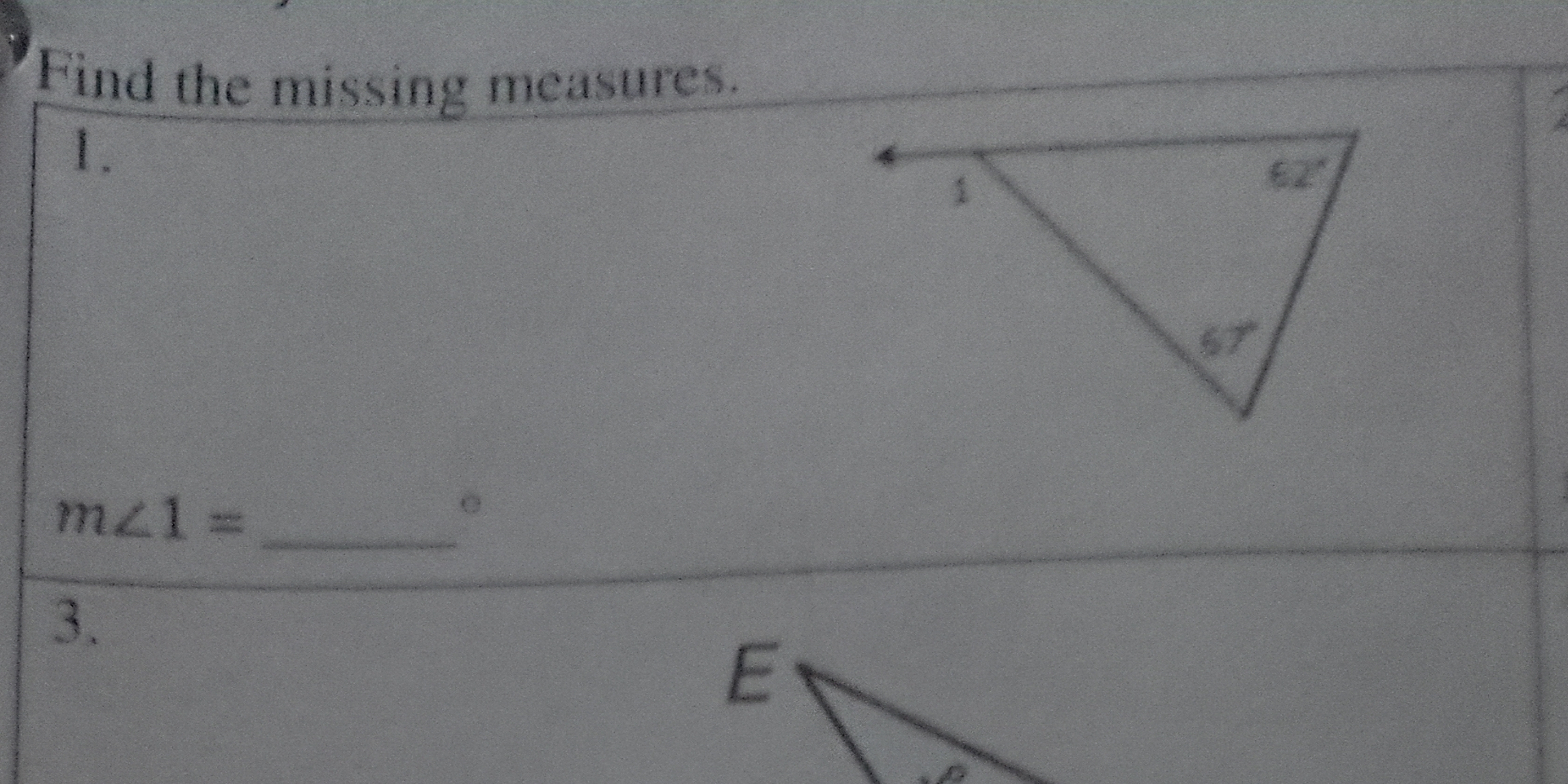
Find the missing measures. m∠1 = ___°.
Understand the Problem
The question asks to find the missing measure of angle 1 in a triangle, given two angles: 62° and 67°. To find the missing angle, we can use the property that the sum of angles in a triangle is always 180°.
Answer
$m\angle 1 = 51°$
Answer for screen readers
$m\angle 1 = 51°$
Steps to Solve
- Identify the known angles
In the triangle, we have angle measures of 62° and 67°.
- Use the triangle angle sum property
The sum of the angles in a triangle is always 180°. We can write the equation:
$$ m\angle 1 + 62° + 67° = 180° $$
- Combine the known angles
Add the two known angles together:
$$ 62° + 67° = 129° $$
- Subtract from 180° to find the missing angle
Now, substitute the sum of the known angles back into the equation:
$$ m\angle 1 + 129° = 180° $$
To isolate $m\angle 1$, subtract 129° from both sides:
$$ m\angle 1 = 180° - 129° $$
- Calculate the value
Finally, compute the result:
$$ m\angle 1 = 51° $$
$m\angle 1 = 51°$
More Information
The measure of the missing angle in the triangle is 51°. This is derived from the fundamental property of triangles that the sum of all interior angles equals 180°.
Tips
- Forgetting the angle sum property: Always remember that the angles in a triangle must sum to 180°.
- Incorrect arithmetic: Be careful during addition and subtraction to avoid mistakes when calculating the missing angle.
AI-generated content may contain errors. Please verify critical information