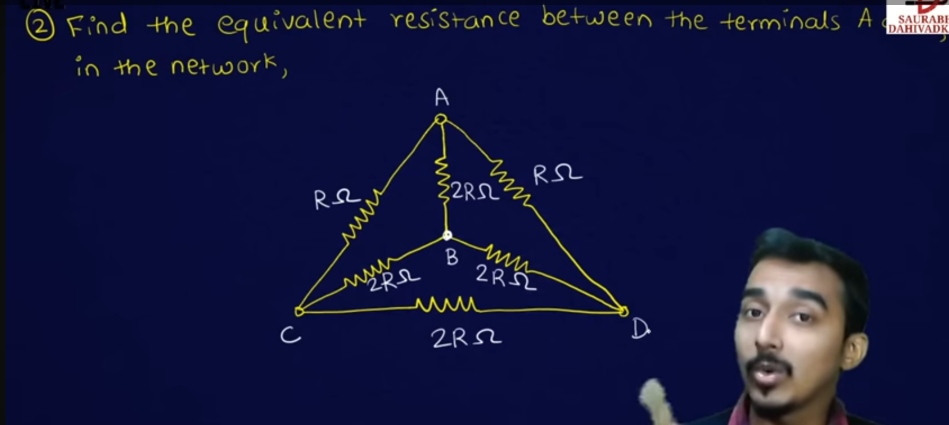
Find the equivalent resistance between the terminals A and D in the network.
Understand the Problem
The question is asking to calculate the equivalent resistance between terminals A and D in a given electrical network consisting of resistors. The goal is to find a single resistance value that represents the network's behavior between these two points.
Answer
The equivalent resistance between terminals A and D is $2R$.
Answer for screen readers
The equivalent resistance between terminals A and D is $2R$.
Steps to Solve
- Identify the resistances in the network The resistances in the network are as follows:
- From A to B: $R$
- From B to C: $2R$
- From B to D: $2R$
- From A to C and A to D: $2R$
- Combine resistances in parallel and series Resistors between points B and C ($2R$) and B and D ($2R$) are in parallel. To find the equivalent resistance $R_{BCD}$, use the formula for parallel resistors:
$$ \frac{1}{R_{BCD}} = \frac{1}{2R} + \frac{1}{2R} $$
- Calculate the equivalent resistance between B and C/D Calculating $R_{BCD}$, we get:
$$ \frac{1}{R_{BCD}} = \frac{1}{2R} + \frac{1}{2R} = \frac{2}{2R} = \frac{1}{R} $$
Thus,
$$ R_{BCD} = R $$
- Combine R with the resistances from A to B Now, combine $R_{BCD}$ with the resistance $R$ from A to B (which are in series):
$$ R_{total} = R + R $$
- Calculate the total equivalent resistance Now, calculate the total resistance:
$$ R_{total} = 2R $$
The equivalent resistance between terminals A and D is $2R$.
More Information
In this configuration, the network can often lead to interesting results, such as simplifications due to symmetry and parallel combinations.
Tips
- Failing to check for parallel and series configurations can lead to incorrect calculations.
- Not simplifying the fractions correctly when combining resistances in parallel.