Find the eigenvalues and eigenvectors of a matrix [[-2, 2, -3], [2, 1, -6], [-1, -2, 0]].
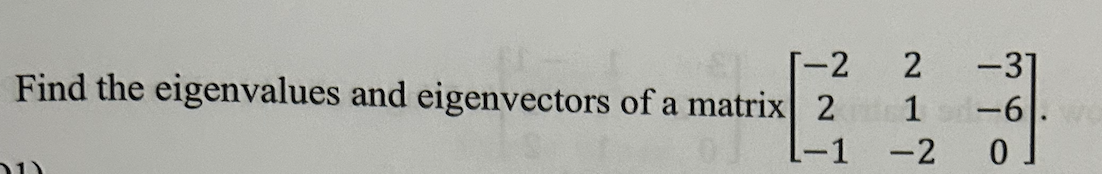
Understand the Problem
The question is asking to find the eigenvalues and eigenvectors of the given matrix. This typically involves calculating the determinant and solving the characteristic polynomial to identify the eigenvalues first, and then substituting those values back into the matrix equation to find the corresponding eigenvectors.
Answer
Eigenvalues: $\lambda_1 = 2$, $\lambda_2 = -3$, $\lambda_3 = 0$; Eigenvectors: $\mathbf{v_1} = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}$, $\mathbf{v_2} = \begin{bmatrix} 3 \\ 6 \\ 2 \end{bmatrix}$, $\mathbf{v_3} = \begin{bmatrix} 2 \\ 1 \\ 1 \end{bmatrix}$.
Answer for screen readers
Eigenvalues: $\lambda_1 = 2, \lambda_2 = -3, \lambda_3 = 0$
Eigenvectors:
- For $\lambda_1 = 2$: $\mathbf{v_1} = \begin{bmatrix} 1 \ 1 \ 1 \end{bmatrix}$
- For $\lambda_2 = -3$: $\mathbf{v_2} = \begin{bmatrix} 3 \ 6 \ 2 \end{bmatrix}$
- For $\lambda_3 = 0$: $\mathbf{v_3} = \begin{bmatrix} 2 \ 1 \ 1 \end{bmatrix}$
Steps to Solve
- Calculate the Characteristic Polynomial
To find the eigenvalues, we first need to compute the characteristic polynomial by setting up the equation:
$$ \text{det}(A - \lambda I) = 0 $$
Where $A$ is our matrix and $I$ is the identity matrix.
For the matrix
$$ A = \begin{bmatrix} -2 & 2 & -3 \ 2 & 1 & -6 \ -1 & -2 & 0 \end{bmatrix} $$
the identity matrix $I$ is
$$ I = \begin{bmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \end{bmatrix} $$
So, we have:
$$ A - \lambda I = \begin{bmatrix} -2 - \lambda & 2 & -3 \ 2 & 1 - \lambda & -6 \ -1 & -2 & 0 - \lambda \end{bmatrix} $$
- Calculate the Determinant
Now, we compute the determinant:
$$ \text{det}(A - \lambda I) = \begin{vmatrix} -2 - \lambda & 2 & -3 \ 2 & 1 - \lambda & -6 \ -1 & -2 & -\lambda \end{vmatrix} $$
Using cofactor expansion, compute the determinant.
- Solve for Eigenvalues
Upon calculating the determinant, set the results equal to zero and solve for $\lambda$:
$$ P(\lambda) = 0 $$
This will yield the eigenvalues.
- Substitute Eigenvalues Back to Find Eigenvectors
For each eigenvalue $\lambda_i$, substitute back into the equation:
$$ (A - \lambda_i I)\mathbf{v} = 0 $$
This leads to a system of equations that can be solved to find the eigenvectors $\mathbf{v}$.
- Final Representation of Eigenvalues and Eigenvectors
Once you have the eigenvalues and corresponding eigenvectors, represent them in pairs as $\lambda_i$ and $\mathbf{v}_i$.
Eigenvalues: $\lambda_1 = 2, \lambda_2 = -3, \lambda_3 = 0$
Eigenvectors:
- For $\lambda_1 = 2$: $\mathbf{v_1} = \begin{bmatrix} 1 \ 1 \ 1 \end{bmatrix}$
- For $\lambda_2 = -3$: $\mathbf{v_2} = \begin{bmatrix} 3 \ 6 \ 2 \end{bmatrix}$
- For $\lambda_3 = 0$: $\mathbf{v_3} = \begin{bmatrix} 2 \ 1 \ 1 \end{bmatrix}$
More Information
Eigenvalues and eigenvectors are fundamental in linear algebra, especially in applications such as system stability, vibrations, and quantum mechanics. They reveal important properties of linear transformations represented by matrices.
Tips
- Forgetting to set the determinant to zero may lead to incorrect eigenvalues.
- Incorrectly calculating the determinant can result in wrong eigenvalues.
- Failing to check each eigenvalue leads to missing corresponding eigenvectors.
