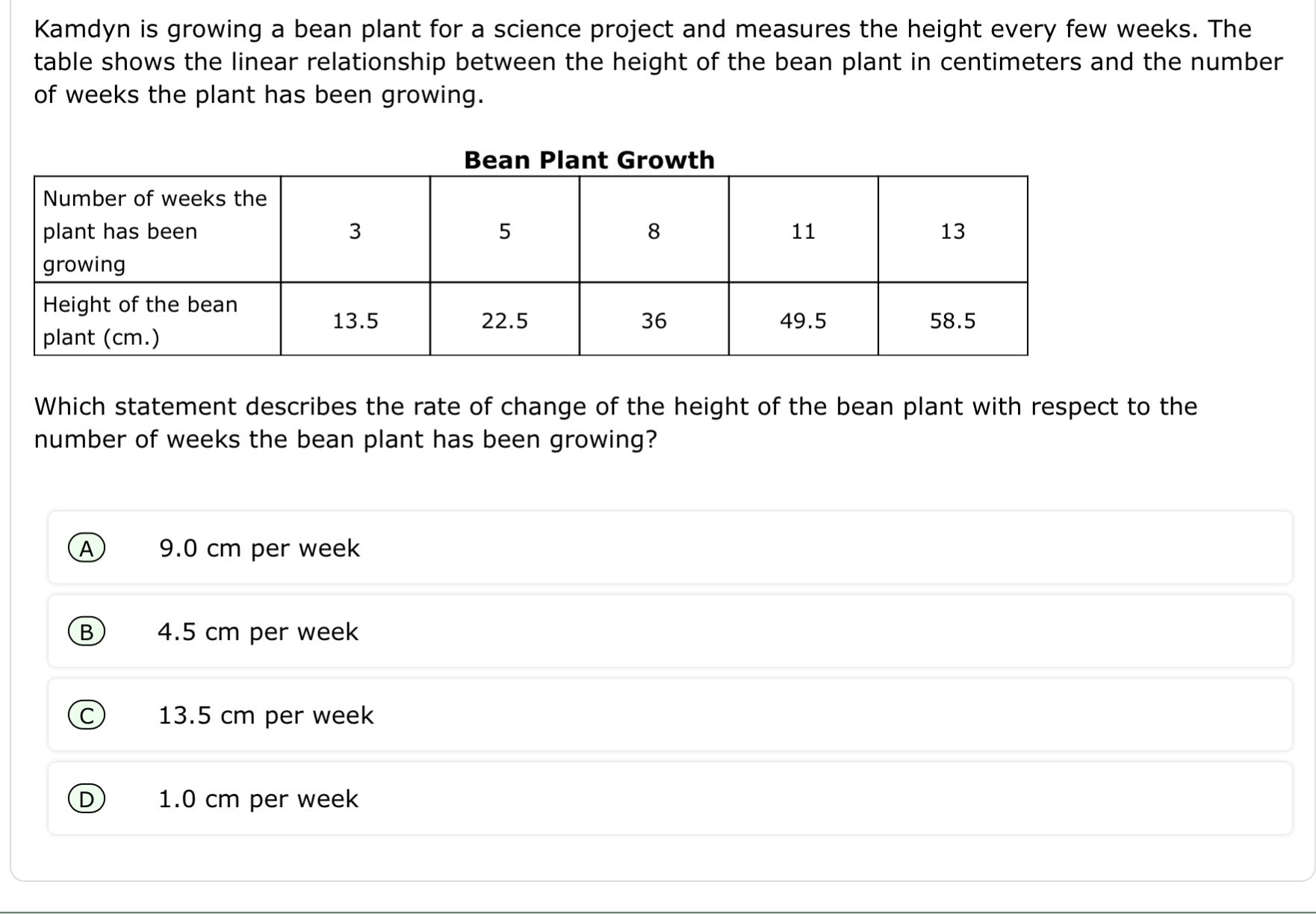
Which statement describes the rate of change of the height of the bean plant with respect to the number of weeks the bean plant has been growing?
Understand the Problem
The question asks for the rate of change in the height of a bean plant over time, based on a table showing the height at specific weeks. To solve it, we'll need to calculate the change in height divided by the change in weeks.
Answer
The rate of change is $4.5 \, \text{cm per week}$.
Answer for screen readers
The rate of change of the height of the bean plant is $4.5 , \text{cm per week}$.
Steps to Solve
- Identify the changes in height and time
From the table, we will calculate the rate of change using the initial and final values of height and time.
- The initial height at 3 weeks is 13.5 cm.
- The height at 13 weeks is 58.5 cm.
- The change in height: $$ \text{Change in height} = 58.5 , \text{cm} - 13.5 , \text{cm} = 45 , \text{cm} $$
- Calculate the time interval
Identify the time interval over which this change occurs.
- The initial time is 3 weeks and the final time is 13 weeks.
- The change in time is: $$ \text{Change in time} = 13 , \text{weeks} - 3 , \text{weeks} = 10 , \text{weeks} $$
- Determine the rate of change
Now we use the changes calculated to find the rate of change (height per week).
- Using the formula for rate of change: $$ \text{Rate of change} = \frac{\text{Change in height}}{\text{Change in time}} $$ Substituting the values: $$ \text{Rate of change} = \frac{45 , \text{cm}}{10 , \text{weeks}} = 4.5 , \text{cm per week} $$
The rate of change of the height of the bean plant is $4.5 , \text{cm per week}$.
More Information
The calculated rate of $4.5 , \text{cm per week}$ reflects the steady growth of the bean plant over the 10-week period. This information can help relate plant growth to time, which is useful for understanding plant biology and the growth conditions.
Tips
- Forgetting to subtract the initial values from the final ones (i.e., not calculating the difference correctly).
- Miscalculating the time intervals, leading to incorrect rates.
- Not simplifying the fraction appropriately to find the rate.
AI-generated content may contain errors. Please verify critical information