Find the domain and range of the following functions: i) f(x) = x + 2, ii) f(x) = x^2, iii) f(x) = 2x + 3, iv) f(x) = sin(x).

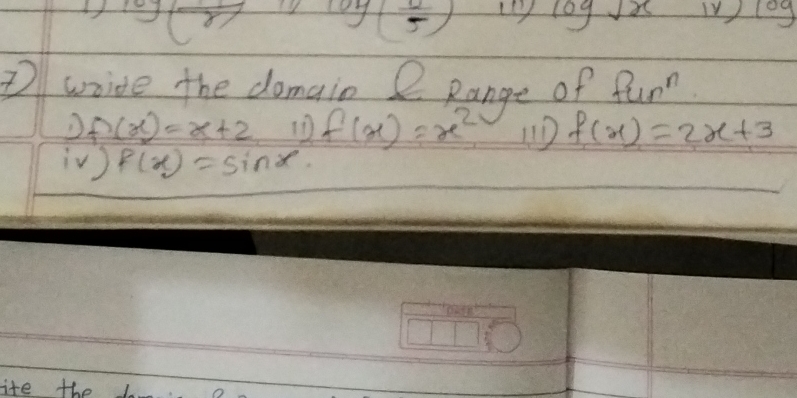
Understand the Problem

The question is asking to find the domain and range of four given functions. This involves determining the set of input values (domain) for which each function is defined and the corresponding output values (range) that the function can take.

Answer

- i) $D: (-\infty, \infty)$, $R: (-\infty, \infty)$ - ii) $D: (-\infty, \infty)$, $R: [0, \infty)$ - iii) $D: (-\infty, \infty)$, $R: (-\infty, \infty)$ - iv) $D: (-\infty, \infty)$, $R: [-1, 1]$

Steps to Solve

Determine the domain of each function
- For $f(x) = x + 2$: The domain is all real numbers, so $D(f) = (-\infty, \infty)$.
- For $f(x) = x^2$: The domain is also all real numbers, so $D(f) = (-\infty, \infty)$.
- For $f(x) = 2x + 3$: The domain is all real numbers, so $D(f) = (-\infty, \infty)$.
- For $f(x) = \sin(x)$: The domain is all real numbers, so $D(f) = (-\infty, \infty)$.
Determine the range of each function
- For $f(x) = x + 2$: The range is also all real numbers, so $R(f) = (-\infty, \infty)$.
- For $f(x) = x^2$: The range is $[0, \infty)$, since the smallest value is $0$ (when $x=0$).
- For $f(x) = 2x + 3$: The range is all real numbers, so $R(f) = (-\infty, \infty)$.
- For $f(x) = \sin(x)$: The range is $[-1, 1]$, as sine oscillates between these values.
Compile the results
- Domain and range summary:
  - i) Domain: $(-\infty, \infty)$; Range: $(-\infty, \infty)$
  - ii) Domain: $(-\infty, \infty)$; Range: $[0, \infty)$
  - iii) Domain: $(-\infty, \infty)$; Range: $(-\infty, \infty)$
  - iv) Domain: $(-\infty, \infty)$; Range: $[-1, 1]$

i) Domain: $(-\infty, \infty)$; Range: $(-\infty, \infty)$
ii) Domain: $(-\infty, \infty)$; Range: $[0, \infty)$
iii) Domain: $(-\infty, \infty)$; Range: $(-\infty, \infty)$
iv) Domain: $(-\infty, \infty)$; Range: $[-1, 1]$

More Information

These functions represent common forms encountered in algebra and trigonometry. The linear functions (i, iii) and the quadratic function (ii) have domains of all real numbers and display particular ranges depending on their structure. The trigonometric function (iv) has a restricted range due to the periodic nature of sine.

Tips

Confusing domain and range: The domain refers to input values, while the range refers to output values. Keep them distinct.
Overlooking the minimum value for quadratic functions: The range must start from the vertex value when maximum/minimum occurs.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!