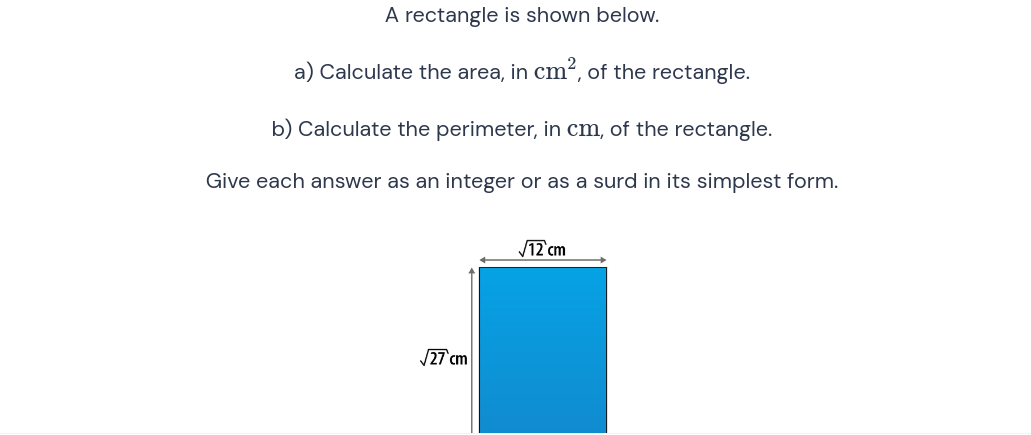
Calculate the area, in cm², of the rectangle. Calculate the perimeter, in cm, of the rectangle. Give each answer as an integer or as a surd in its simplest form.
Understand the Problem
The question is asking to calculate the area and perimeter of a rectangle using the given dimensions. It requires finding the area in square centimeters and the perimeter in centimeters, and presenting the answers as either integers or in simplest surd form.
Answer
Area: $36\sqrt{3}$ cm²; Perimeter: $24 + 6\sqrt{3}$ cm.
Answer for screen readers
The area of the rectangle is $36\sqrt{3}$ cm² and the perimeter is $24 + 6\sqrt{3}$ cm.
Steps to Solve
- Identify the dimensions of the rectangle
The dimensions of the rectangle are given as:
- Length (l) = $12$ cm
- Width (w) = $\sqrt{27}$ cm
- Calculate the area of the rectangle
The area ($A$) of a rectangle can be calculated using the formula: $$ A = l \times w $$ Substituting the values: $$ A = 12 \times \sqrt{27} $$
- Simplify the area calculation
Since $\sqrt{27} = \sqrt{9 \times 3} = 3\sqrt{3}$, we substitute this back into the area equation: $$ A = 12 \times 3\sqrt{3} = 36\sqrt{3} \text{ cm}^2 $$
- Calculate the perimeter of the rectangle
The perimeter ($P$) of a rectangle can be calculated using the formula: $$ P = 2(l + w) $$ Substituting in the values: $$ P = 2(12 + \sqrt{27}) $$
- Simplify the perimeter calculation
Using $\sqrt{27} = 3\sqrt{3}$: $$ P = 2(12 + 3\sqrt{3}) = 24 + 6\sqrt{3} \text{ cm} $$
The area of the rectangle is $36\sqrt{3}$ cm² and the perimeter is $24 + 6\sqrt{3}$ cm.
More Information
The area of the rectangle, found by multiplying its length and width, involves simplification of square roots. The perimeter formula sums the lengths of all sides and is then simplified for clarity.
Tips
- Forgetting to simplify the square root in the area calculation.
- Not doubling both dimensions when calculating the perimeter.
AI-generated content may contain errors. Please verify critical information