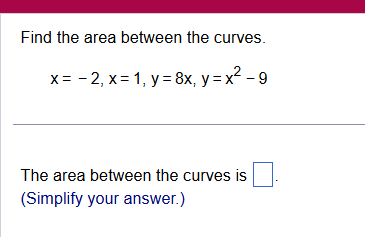
Find the area between the curves: x = -2, x = 1, y = 8x, y = x^2 - 9.

Steps to Solve

1. Identify the curves and intervals

The curves given are ( y = 8x ) and ( y = x^2 - 9 ). We need to find their intersections to determine the area between them from ( x = -2 ) to ( x = 1 ).

2. Find the points of intersection

Set the equations equal to each other:

[ 8x = x^2 - 9 ]

Rearranging gives:

[ x^2 - 8x - 9 = 0 ]

Now, use the quadratic formula ( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} ) where ( a = 1, b = -8, c = -9 ):

[ x = \frac{8 \pm \sqrt{(-8)^2 - 4 \cdot 1 \cdot (-9)}}{2 \cdot 1} \ x = \frac{8 \pm \sqrt{64 + 36}}{2} \ x = \frac{8 \pm \sqrt{100}}{2} \ x = \frac{8 \pm 10}{2} ]

Thus, the solutions are:

[ x = 9 \quad \text{and} \quad x = -1 ]

3. Determine which curve is on top

Evaluate values between ( x = -2 ) and ( x = 1 ):

• At ( x = -2 ):

[ y = 8(-2) = -16 \quad \text{and} \quad y = (-2)^2 - 9 = -5 ]

Thus, ( y = x^2 - 9 ) is on top.

• At ( x = 0 ):

[ y = 8(0) = 0 \quad \text{and} \quad y = (0)^2 - 9 = -9 ]

Again, ( y = x^2 - 9 ) is on top.

4. Set up the integral for the area

We calculate the area ( A ) between the curves from ( x = -2 ) to ( x = 1 ):

[ A = \int_{-2}^{1} ((x^2 - 9) - (8x)) , dx = \int_{-2}^{1} (x^2 - 8x - 9) , dx ]

5. Evaluate the integral

First, integrate:

[ \int (x^2 - 8x - 9) , dx = \frac{x^3}{3} - 4x^2 - 9x + C ]

Now, evaluate from ( -2 ) to ( 1 ):

[ A = \left[ \frac{(1)^3}{3} - 4(1)^2 - 9(1) \right] - \left[ \frac{(-2)^3}{3} - 4(-2)^2 - 9(-2) \right] ]

Calculating these:

For ( x = 1 ):

[ = \frac{1}{3} - 4 - 9 = \frac{1}{3} - 13 = \frac{1 - 39}{3} = \frac{-38}{3} ]

For ( x = -2 ):

[ = \frac{-8}{3} - 16 + 18 = \frac{-8}{3} + 2 = \frac{-8 + 6}{3} = \frac{-2}{3} ]

Thus,

[ A = \left(\frac{-38}{3}\right) - \left(\frac{-2}{3}\right) = \frac{-38 + 2}{3} = \frac{-36}{3} = -12 ]

Taking the absolute value:

[ \text{Area} = 12 ]