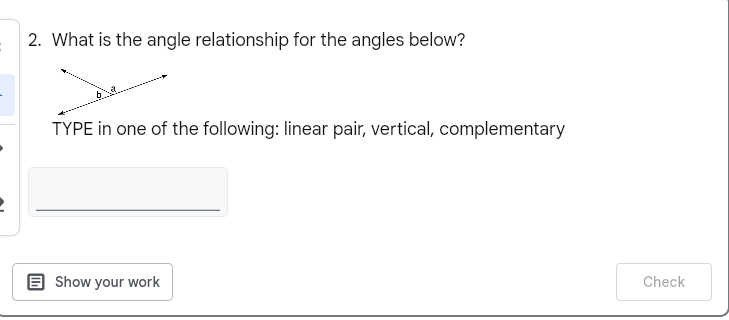
What is the angle relationship for the angles below? TYPE in one of the following: linear pair, vertical, complementary.
Understand the Problem
The question is asking to identify the relationship between two angles based on their positions, specifically whether they form a linear pair, are vertical angles, or are complementary.
Answer
Vertical angles.
Answer for screen readers
The angle relationship is vertical angles.
Steps to Solve
-
Identify the Angles The angles represented are formed by two intersecting lines. Let's label the angles as ( \angle a ) and ( \angle b ).
-
Determine the Relationship Examine the positions of angles ( a ) and ( b ).
-
Evaluate if they are Vertical Angles If ( \angle a ) and ( \angle b ) are opposite each other and formed by two intersecting lines, then they are vertical angles.
-
Evaluate if they are a Linear Pair If the sum of angles ( a ) and ( b ) equals ( 180^\circ ) (i.e., they are supplementary), then they form a linear pair.
-
Check for Complementary Angles If angles ( a ) and ( b ) sum to ( 90^\circ ), they are considered complementary.
The angle relationship is vertical angles.
More Information
Vertical angles are always equal in measure and are formed when two lines intersect.
Tips
- Confusing vertical angles with linear pairs. Remember, vertical angles are opposite each other at the intersection, while linear pairs are adjacent and sum up to ( 180^\circ ).
- Misidentifying complementary angles. It's crucial that their sum equals ( 90^\circ ).
AI-generated content may contain errors. Please verify critical information