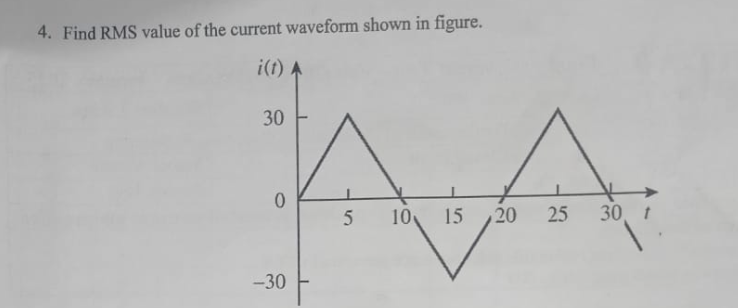
Find RMS value of the current waveform shown in figure.

Steps to Solve

1. Identify the waveform segments

The given waveform consists of two repeating segments:

• A triangular wave from 0 to 15 seconds: peaks at $30 , \text{A}$ and drops to $0 , \text{A}$ at $5 , \text{s}$ and $15 , \text{s}$.
• A negative triangular wave from 15 to 30 seconds: peaks at $-30 , \text{A}$ and drops to $0 , \text{A}$ at $20 , \text{s}$ and $30 , \text{s}$.

2. Calculate the RMS value for one segment of the waveform

The RMS value for a triangular waveform is given by the formula:

$$ I_{\text{RMS}} = \frac{I_{\text{peak}}}{\sqrt{3}} $$

For the positive segment, $I_{\text{peak}} = 30 , \text{A}$:

$$ I_{\text{RMS, positive}} = \frac{30}{\sqrt{3}} $$

3. Calculate the RMS value for the negative segment

Using the same formula, for the negative segment where $I_{\text{peak}} = 30 , \text{A}$ (but negative):

$$ I_{\text{RMS, negative}} = \frac{30}{\sqrt{3}} $$

4. Combine the RMS values of both segments

Since both segments contribute equally to the RMS calculation over one complete cycle, the overall RMS value of the waveform is the same as the RMS of one segment:

$$ I_{\text{RMS}} = I_{\text{RMS, positive}} = I_{\text{RMS, negative}} = \frac{30}{\sqrt{3}} $$

5. Calculate the numerical value

To find the numerical value:

$$ I_{\text{RMS}} = \frac{30}{\sqrt{3}} \approx 17.32 , \text{A} $$