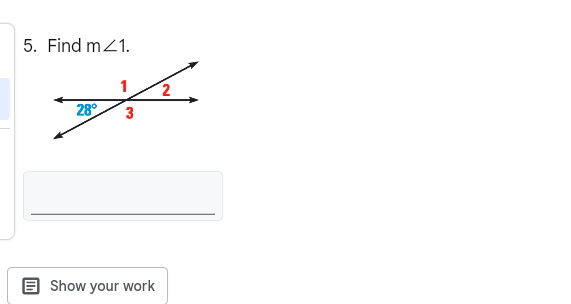
Find m∠1.
Understand the Problem
The question is asking for the measure of angle 1, given that angle 3 is 28 degrees. The context suggests using properties of parallel lines and angles formed by a transversal.
Answer
The measure of angle 1 is \( m\angle 1 = 152^\circ \).
Answer for screen readers
The measure of angle 1 is ( m\angle 1 = 152^\circ ).
Steps to Solve
- Identify Angle Relationships
Given that angles 2 and 3 are corresponding angles formed by a transversal intersecting parallel lines, we can establish that they are equal. Thus, we have: $$ m\angle 2 = m\angle 3 = 28^\circ $$
- Apply the Linear Pair Postulate
Angles 1 and 2 form a linear pair because they are adjacent angles on a straight line. Therefore, their measures add up to (180^\circ): $$ m\angle 1 + m\angle 2 = 180^\circ $$
- Substituting Known Values
Now substitute the measure of angle 2: $$ m\angle 1 + 28^\circ = 180^\circ $$
- Solve for Angle 1
Now, isolate (m\angle 1) by subtracting (28^\circ) from both sides: $$ m\angle 1 = 180^\circ - 28^\circ $$ $$ m\angle 1 = 152^\circ $$
The measure of angle 1 is ( m\angle 1 = 152^\circ ).
More Information
In parallel lines cut by a transversal, corresponding angles are equal, and angles on a straight line always sum to (180^\circ). This problem demonstrates the application of those properties in geometry.
Tips
- Confusing corresponding angles with alternate interior angles. Remember: corresponding angles (like angles 2 and 3) are equal when lines are parallel.
- Not recognizing that adjacent angles on a straight line sum to (180^\circ).
AI-generated content may contain errors. Please verify critical information