Find dy/dx for the given functions: 1) y = √(4 + 2x) 2) y = (4 + sin²(3x))⁵ 3) x² + cot(xy) = 17 4) y = cot⁻¹(e^(5x))
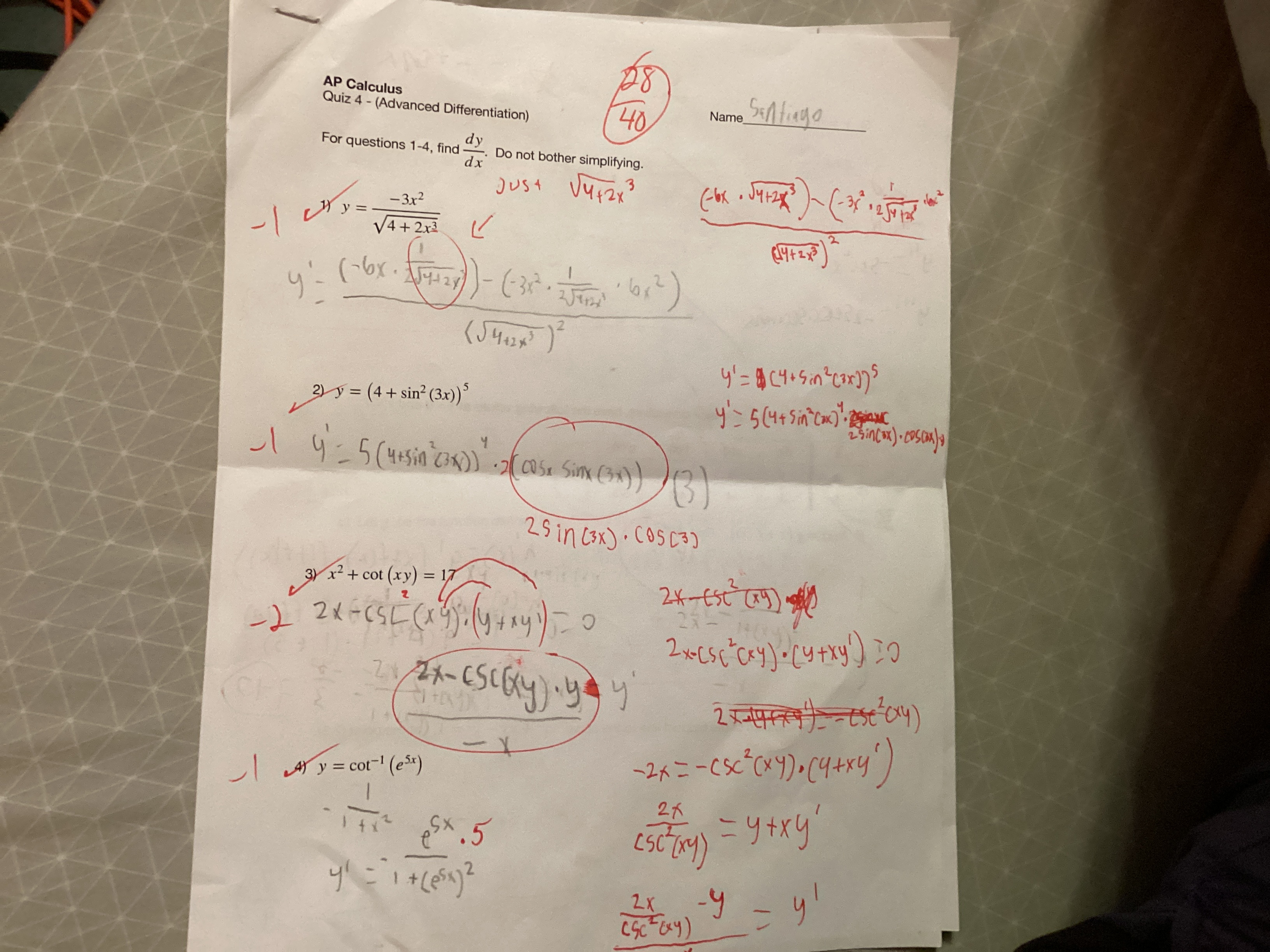
Understand the Problem
The question involves finding the derivative of various functions using advanced differentiation techniques. It requires applying rules such as the chain rule and implicit differentiation.
Answer
1. $y' = -\frac{1}{\sqrt{4 + 2x}^3}$ 2. $y' = 30(4 + \sin^2(3x))^4 \sin(3x) \cos(3x)$ 3. $y' = \frac{-2x}{\csc^2(xy)(x)} - y$ 4. $y' = -\frac{5e^{5x}}{1 + e^{10x}}$
Answer for screen readers
- $$ y' = -\frac{1}{\sqrt{4 + 2x}^3} $$
- $$ y' = 30(4 + \sin^2(3x))^4 \sin(3x) \cos(3x) $$
- $$ y' = \frac{-2x}{\csc^2(xy)(x)} - y $$
- $$ y' = -\frac{5e^{5x}}{1 + e^{10x}} $$
Steps to Solve
- Find the derivative of ( y = \frac{1}{\sqrt{4 + 2x}} )
Use the chain rule. Start by rewriting the function as:
$$ y = (4 + 2x)^{-1/2} $$
Then apply the chain rule:
$$ y' = -\frac{1}{2} (4 + 2x)^{-3/2} \cdot (2) $$
- Differentiate ( y = (4 + \sin^2(3x))^5 )
Use the chain rule again. Let ( u = 4 + \sin^2(3x) ):
$$ y = u^5 $$
Then:
$$ y' = 5u^4 \cdot \frac{du}{dx} $$
Next, find ( \frac{du}{dx} ):
$$ \frac{du}{dx} = 2\sin(3x)(3\cos(3x)) = 6\sin(3x)\cos(3x) $$
Combine results:
$$ y' = 5(4 + \sin^2(3x))^4 \cdot 6\sin(3x)\cos(3x) $$
- Differentiate ( x^2 + \cot(xy) = 17 )
Apply implicit differentiation. Differentiate each term:
$$ 2x + \frac{d}{dx}[\cot(xy)] = 0 $$
Using the product rule on ( \cot(xy) ), we get:
$$ -\csc^2(xy)(y + x y') = 0 $$
Solve for ( y' ):
$$ 2x - \csc^2(xy)(y + xy') = 0 $$
- Differentiate ( y = \cot^{-1}(e^{5x}) )
Use the chain rule:
$$ y' = -\frac{1}{1 + (e^{5x})^2} \cdot \frac{d}{dx}(e^{5x}) $$
Calculate:
$$ \frac{d}{dx}(e^{5x}) = 5e^{5x} $$
So:
$$ y' = -\frac{5e^{5x}}{1 + e^{10x}} $$
- $$ y' = -\frac{1}{\sqrt{4 + 2x}^3} $$
- $$ y' = 30(4 + \sin^2(3x))^4 \sin(3x) \cos(3x) $$
- $$ y' = \frac{-2x}{\csc^2(xy)(x)} - y $$
- $$ y' = -\frac{5e^{5x}}{1 + e^{10x}} $$
More Information
The derivatives above demonstrate the application of the chain rule, product rule, and implicit differentiation techniques. These are fundamental concepts in calculus that help in understanding rate changes of complex functions.
Tips
- Omitting negative signs: Ensure to keep track of negative signs, especially when differentiating inverse functions.
- Misapplying product and chain rules: Be careful to differentiate each component correctly, particularly when using both rules in a single step.
AI-generated content may contain errors. Please verify critical information