Find an elementary matrix E such that EA = B, where A = [[3, -4], [2, 5]] and B = [[3, -4], [-4, 13]].
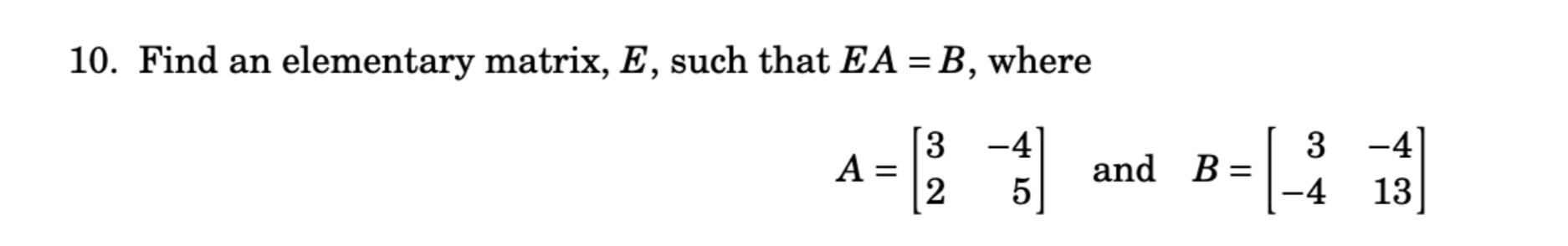
Understand the Problem
The question is asking for an elementary matrix E such that when it is multiplied by matrix A, it results in matrix B. To solve this, we need to determine the transformation represented by E that achieves this multiplication.
Answer
The elementary matrix is \[ E = \begin{bmatrix} 1 & 0 \\ -2 & 1 \end{bmatrix} \]
Answer for screen readers
The elementary matrix ( E ) is
[ E = \begin{bmatrix} 1 & 0 \ -2 & 1 \end{bmatrix} ]
Steps to Solve
- Identify Matrix A and B
The given matrices are:
[ A = \begin{bmatrix} 3 & -4 \ 2 & 5 \end{bmatrix}, \quad B = \begin{bmatrix} 3 & -4 \ -4 & 13 \end{bmatrix} ]
- Determine the Transformation
We need to find an elementary matrix ( E ) such that ( E A = B ). This can involve either row operations or scaling. Let's analyze what changes from ( A ) to ( B ).
- Set Up the Equation
Using the matrix equation,
[ E A = B ]
we substitute for ( E ):
[ E = B A^{-1} ]
- Calculate the Inverse of A
Now, we find the inverse of ( A ).
The formula for the inverse of a 2x2 matrix ( \begin{bmatrix} a & b \ c & d \end{bmatrix} ) is:
[ \text{Inverse} = \frac{1}{ad - bc} \begin{bmatrix} d & -b \ -c & a \end{bmatrix} ]
For ( A ), ( a = 3, b = -4, c = 2, d = 5 ):
[ ad - bc = 3 \cdot 5 - (-4) \cdot 2 = 15 + 8 = 23 ]
Thus, the inverse of ( A ) is:
[ A^{-1} = \frac{1}{23} \begin{bmatrix} 5 & 4 \ -2 & 3 \end{bmatrix} = \begin{bmatrix} \frac{5}{23} & \frac{4}{23} \ -\frac{2}{23} & \frac{3}{23} \end{bmatrix} ]
- Compute E
Now we compute ( E ):
[ E = B A^{-1} = \begin{bmatrix} 3 & -4 \ -4 & 13 \end{bmatrix} \begin{bmatrix} \frac{5}{23} & \frac{4}{23} \ -\frac{2}{23} & \frac{3}{23} \end{bmatrix} ]
Perform the multiplication:
First row:
[ \begin{bmatrix} 3 \cdot \frac{5}{23} + (-4) \cdot \left(-\frac{2}{23}\right) & 3 \cdot \frac{4}{23} + (-4) \cdot \frac{3}{23} \end{bmatrix} ] [ = \begin{bmatrix} \frac{15}{23} + \frac{8}{23} & \frac{12}{23} - \frac{12}{23} \end{bmatrix} = \begin{bmatrix} \frac{23}{23} & 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 \end{bmatrix} ]
Second row:
[ \begin{bmatrix} -4 \cdot \frac{5}{23} + 13 \cdot \left(-\frac{2}{23}\right) & -4 \cdot \frac{4}{23} + 13 \cdot \frac{3}{23} \end{bmatrix} ] [ = \begin{bmatrix} -\frac{20}{23} - \frac{26}{23} & -\frac{16}{23} + \frac{39}{23} \end{bmatrix} = \begin{bmatrix} -\frac{46}{23} & \frac{23}{23} \end{bmatrix} = \begin{bmatrix} -2 & 1 \end{bmatrix} ]
Thus,
[ E = \begin{bmatrix} 1 & 0 \ -2 & 1 \end{bmatrix} ]
The elementary matrix ( E ) is
[ E = \begin{bmatrix} 1 & 0 \ -2 & 1 \end{bmatrix} ]
More Information
An elementary matrix represents a single elementary row operation applied to an identity matrix. In this case, the operation represented by ( E ) is subtracting 2 times the first row from the second row of matrix ( A ).
Tips
- Not calculating the inverse properly: It's crucial to ensure that the calculation of the inverse uses the correct determinant.
- Forgetting to multiply both rows: When applying the multiplication of matrices, be careful to compute both rows correctly.
- Assuming ( E ) is always a specific form: Elementary matrices can represent different types of operations.
AI-generated content may contain errors. Please verify critical information