Find all real and imaginary solutions to the equation x^3 - 5x^2

Find all real and imaginary solutions to the equation x^3 - 5x^2 - 9x + 45 = 0.

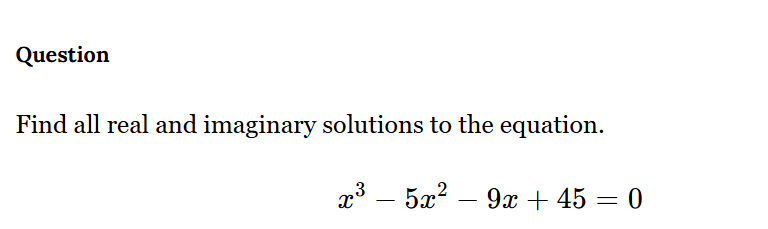
Understand the Problem

The question is asking for all real and imaginary solutions to a given cubic equation. We will find the roots of the polynomial by applying methods such as factoring, using the Rational Root Theorem, or applying numerical methods if necessary.

Answer

The real solutions are $ x = 5, 3, -3 $.

Steps to Solve

Identify Possible Rational Roots

Using the Rational Root Theorem, we can find potential rational roots among the factors of the constant term (45) and the leading coefficient (1). The possible rational roots are:

$$ \pm 1, \pm 3, \pm 5, \pm 9, \pm 15, \pm 45 $$

Test Possible Roots

We will test each possible root using synthetic division to see if any of them yield a remainder of 0.

Testing ( x = 3 ):

Setting up synthetic division:

3 | 1  -5  -9   45
  |     3  -6  -18
  -------------------
    1  -2  -15   27

The remainder is 27, so ( x = 3 ) is not a root.

Testing ( x = 5 ):

Setting up synthetic division:

5 | 1  -5  -9   45
  |     5   0   -45
  -------------------
    1   0  -9    0

The remainder is 0, so ( x = 5 ) is a root.

Factor the Polynomial

Since ( x = 5 ) is a root, we can express the cubic as:

$$ (x - 5)(x^2 - 9) = 0 $$

Find Remaining Roots

Now we can factor ( x^2 - 9 ):

$$ x^2 - 9 = (x - 3)(x + 3) $$

Thus, the polynomial can be fully factored as:

$$ (x - 5)(x - 3)(x + 3) = 0 $$

Solve for Roots

Setting each factor to 0 gives us the solutions:

$$ x - 5 = 0 \Rightarrow x = 5 $$

$$ x - 3 = 0 \Rightarrow x = 3 $$

$$ x + 3 = 0 \Rightarrow x = -3 $$

So, the solutions are ( x = 5, 3, -3 ).

The real solutions to the equation ( x^3 - 5x^2 - 9x + 45 = 0 ) are ( x = 5, 3, -3 ). There are no imaginary solutions.

More Information

This cubic equation has all real roots, and they correspond to the points where the polynomial intersects the x-axis. In general, cubic equations can have up to three real roots, some of which can be repeated, but complex roots appear in conjugate pairs if they exist.

Tips

Forgetting to check all possible rational roots.
Not performing synthetic division correctly, which might lead to incorrect identification of roots.
Failing to factor completely after finding one root.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!