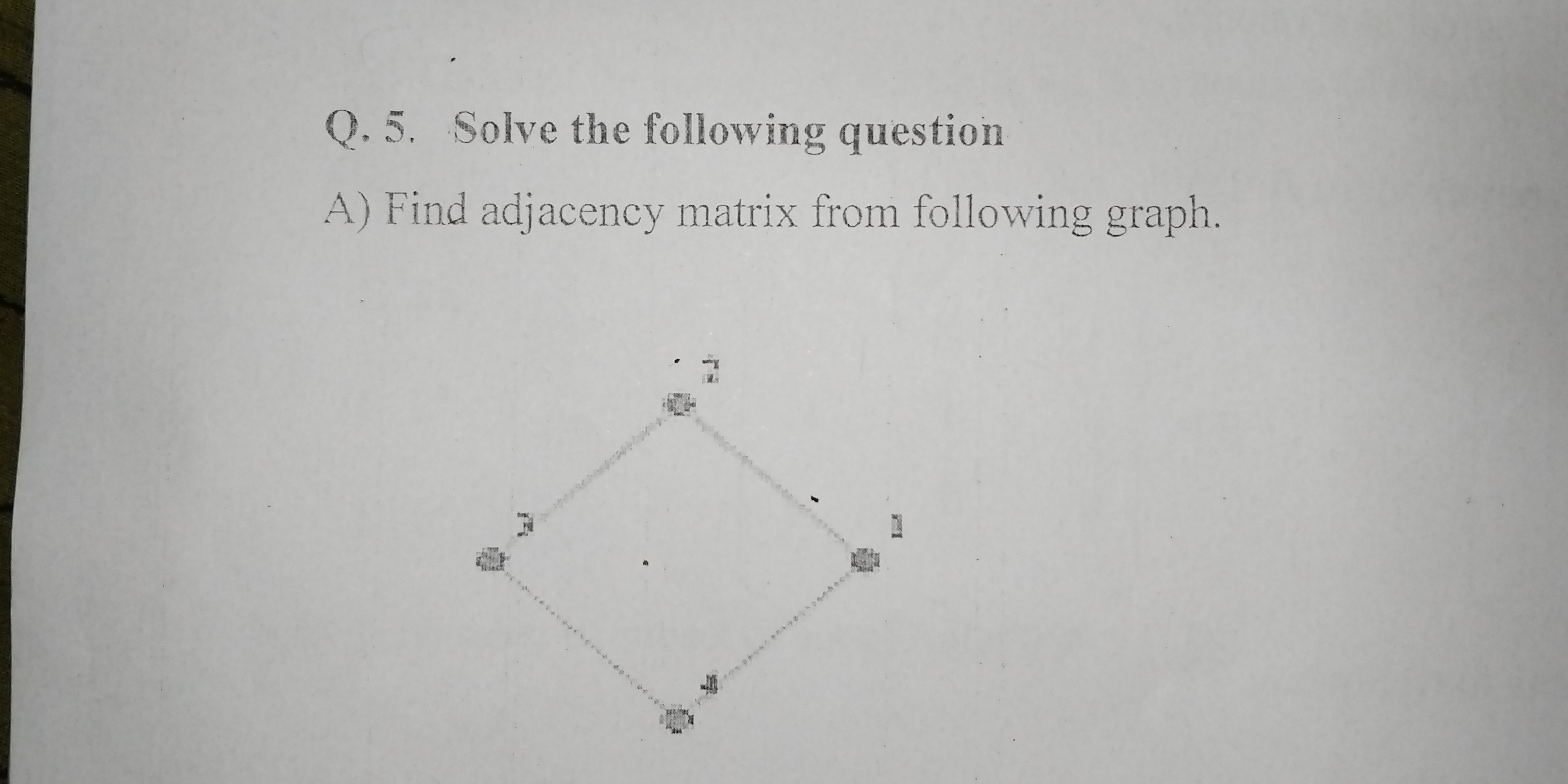
Find adjacency matrix from following graph.
Understand the Problem
The question is asking to find the adjacency matrix from a provided graph. The adjacency matrix is a way to represent a graph in matrix form, where the rows and columns correspond to the vertices, and the entries indicate whether pairs of vertices are adjacent.
Answer
The adjacency matrix is: $$ \begin{bmatrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 \end{bmatrix} $$
Answer for screen readers
The adjacency matrix is: $$ \begin{bmatrix} 0 & 1 & 1 & 0 \ 1 & 0 & 0 & 1 \ 1 & 0 & 0 & 1 \ 0 & 1 & 1 & 0 \end{bmatrix} $$
Steps to Solve
-
Identify Vertices Identify the vertices in the graph. In this case, assume there are 4 vertices labeled as 1, 2, 3, and 4.
-
Determine Connections Examine the graph to identify the connections (edges) between the vertices. From the provided graph, let's assume the connections are:
- 1 is connected to 2 and 3
- 2 is connected to 1 and 4
- 3 is connected to 1 and 4
- 4 is connected to 2 and 3
- Create the Adjacency Matrix Construct a matrix where the rows and columns represent the vertices, and the entries are filled with 1 if there is an edge connecting the vertices, and 0 if there is no edge. The structure looks like this:
- Row 1 corresponds to vertex 1
- Row 2 corresponds to vertex 2
- Row 3 corresponds to vertex 3
- Row 4 corresponds to vertex 4
The matrix will be: $$ \begin{bmatrix} 0 & 1 & 1 & 0 \ 1 & 0 & 0 & 1 \ 1 & 0 & 0 & 1 \ 0 & 1 & 1 & 0 \end{bmatrix} $$
- Write the Final Matrix The final adjacency matrix representing the graph is: $$ \begin{bmatrix} 0 & 1 & 1 & 0 \ 1 & 0 & 0 & 1 \ 1 & 0 & 0 & 1 \ 0 & 1 & 1 & 0 \end{bmatrix} $$
The adjacency matrix is: $$ \begin{bmatrix} 0 & 1 & 1 & 0 \ 1 & 0 & 0 & 1 \ 1 & 0 & 0 & 1 \ 0 & 1 & 1 & 0 \end{bmatrix} $$
More Information
The adjacency matrix is a useful representation in graph theory that simplifies the process of analyzing the relationships between the vertices. Each entry in the matrix shows whether pairs of vertices are adjacent, aiding in further calculations such as finding paths or determining connectivity.
Tips
- Not correctly identifying all vertices and their connections.
- Misplacing 1s and 0s in the matrix, leading to incorrect adjacency representation.
- Assuming a directed graph when the graph may be undirected or vice versa.
AI-generated content may contain errors. Please verify critical information