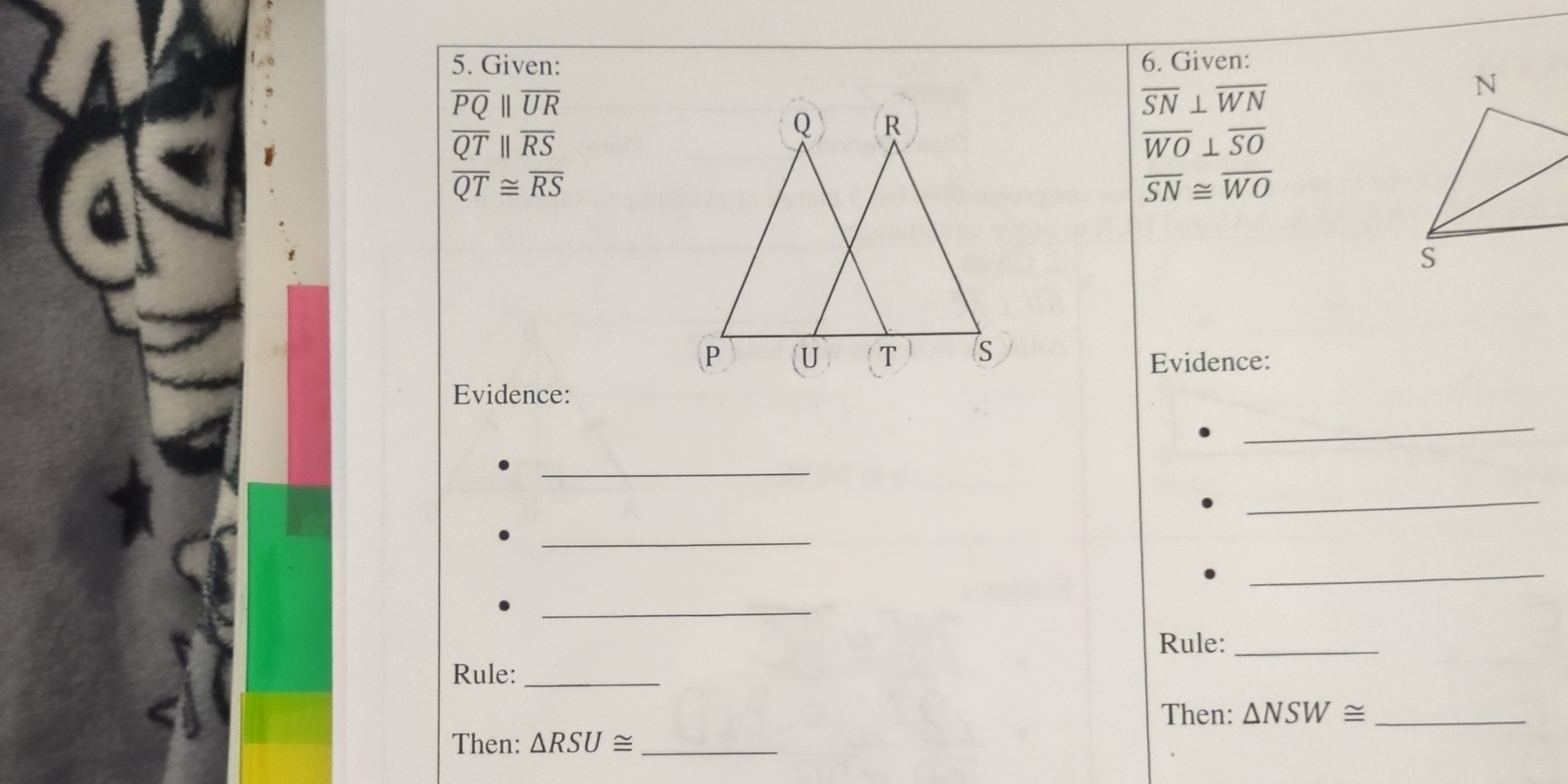
Given PQ || UR, QT || RS, QT ≅ RS. Evidence: (blank). Then: ΔRSU ≅ (blank). Given: SN ⊥ WN, WO ⊥ SO, SN ≅ WO. Evidence: (blank). Then: ΔNSW ≅ (blank).
Understand the Problem
The question presents two geometry problems involving triangles, requiring evidence and rules of congruence to complete each statement about the triangles. The aim is to deduce the congruence of specific triangles based on the given information.
Answer
1. ΔRSU ≅ ΔPQU 2. ΔNSW ≅ ΔOSW
Answer for screen readers
- ΔRSU ≅ ΔPQU
- ΔNSW ≅ ΔOSW
Steps to Solve
- Identify the given information for the first triangle The information states:
- $PQ \parallel UR$ (indicating lines are parallel)
- $QT \parallel RS$ (indicating lines are also parallel)
- $QT \cong RS$ (QT and RS are congruent)
-
Apply the properties of parallel lines Since $PQ \parallel UR$ and $QT \parallel RS$, you can conclude that angles $\angle PQU \cong \angle RUS$ and $\angle QUT \cong \angle SRT$ by the Alternate Interior Angles Theorem.
-
Establish triangle congruence From the information, you have:
- $QT \cong RS$
- $\angle PQU \cong \angle RUS$
- $\angle QUT \cong \angle SRT$
Thus, by the Angle-Side-Angle (ASA) congruence rule, you can write: $$ \Delta RSU \cong \Delta PQU $$
- Identify given information for the second triangle The second part of the problem states:
- $SN \perp WN$ (indicating a right angle)
- $WO \perp SO$ (indicating another right angle)
- $SN \cong WO$ (SN and WO are congruent)
-
Use the properties of right triangles From the perpendicular lines, $\angle NSW \cong \angle OSW$ (both are right angles).
-
Establish second triangle congruence With the information available:
- $SN \cong WO$
- $\angle NSW \cong \angle OSW$
You can apply the Hypotenuse-Leg (HL) theorem for right triangles: $$ \Delta NSW \cong \Delta OSW $$
- ΔRSU ≅ ΔPQU
- ΔNSW ≅ ΔOSW
More Information
In geometry, proving triangle congruence often involves using various theorems such as ASA (Angle-Side-Angle), SSS (Side-Side-Side), and HL (Hypotenuse-Leg for right triangles). The congruence of two triangles leads to the understanding that their corresponding angles and sides are equal, which is fundamental in many geometric proofs and constructions.
Tips
- Ignoring the properties of parallel lines: Always consider the angles formed by parallel lines and transversals when determining triangle congruence.
- Forgetting to identify the correct triangle congruence theorem: Ensure you match the correct theorem (ASA, SSS, or HL) based on the given information.
AI-generated content may contain errors. Please verify critical information