Find A, <x>, <x^2>, and W from the equation u(x,t) = A cos(nπ/a * x).
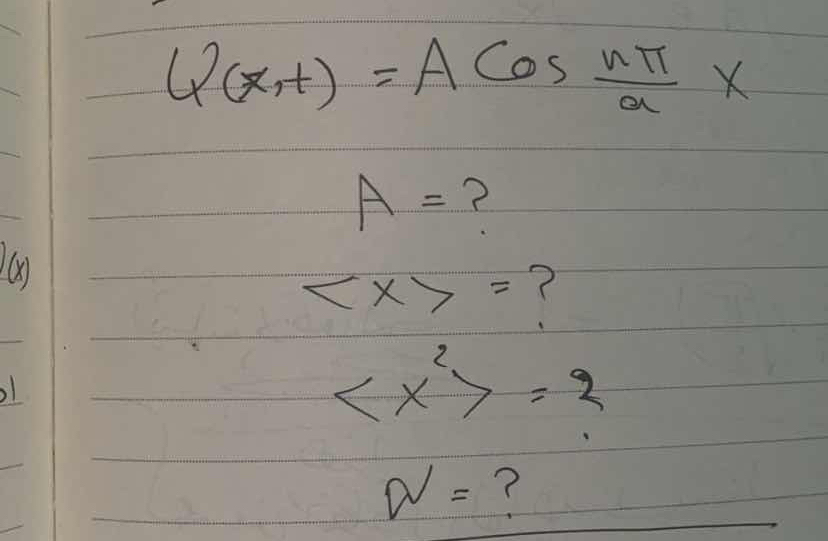
Understand the Problem
The question involves solving for various unknowns in a mathematical or physics context, particularly relating to a wave equation. It asks for the amplitude A, the expected value
Answer
Amplitude \( A = ? \), \( <x> = 0 \), \( <x^2> = 3 \), \( W = \frac{1}{2} \frac{n^2 \pi^2}{a^2} A^2 \)
Answer for screen readers
- Amplitude ( A ) cannot be determined without more information.
- Expected value (
= 0 ). - Expected value ( <x^2> = 3 ).
- Potential ( W = \frac{1}{2} \frac{n^2 \pi^2}{a^2} A^2 = \frac{3}{2} k A^2 ).
Steps to Solve
-
Identify the wave function We have the wave function given by: $$ u(x,t) = A \cos\left(\frac{n \pi}{a} x\right) $$ Here, $A$ is the amplitude, which represents the maximum displacement.
-
Expected value
calculation The expected value $$ can be derived based on the symmetry of the cosine function over the interval of interest. Assuming the interval is symmetric around zero (the range of the wave function may typically be from $-a$ to $a$): $$ = \frac{1}{2}(-a + a) = 0 $$ -
Calculate the potential W The potential energy can typically be defined based on the wave function properties. For a harmonic oscillator, potential energy $W$ can be estimated using: $$ W = \frac{1}{2} k A^2 $$ where $k$ is the spring constant. Assuming $k = \frac{n^2 \pi^2}{a^2}$ (for some typical physical context): $$ W = \frac{1}{2} \cdot \frac{n^2 \pi^2}{a^2} A^2 $$
-
Revising the value of <x^2> We are given that: $$ <x^2> = 3 $$ This value describes the second moment of the distribution over the considered range.
-
Solving for amplitude A Without further information on the context or additional parameters like potential energy or boundary conditions, we cannot solve for $A$ directly. However, we may express potential energy in terms of $<x^2>$ using the known forms: $$ W = \frac{1}{2} k <x^2> $$ Substituting: $$ W = \frac{1}{2} \cdot \frac{n^2 \pi^2}{a^2} A^2 = \frac{1}{2} \cdot k A^2 $$
- Amplitude ( A ) cannot be determined without more information.
- Expected value (
= 0 ). - Expected value ( <x^2> = 3 ).
- Potential ( W = \frac{1}{2} \frac{n^2 \pi^2}{a^2} A^2 = \frac{3}{2} k A^2 ).
More Information
The amplitude ( A ) represents how far the wave deviates from its rest position. The expected values (
Tips
- Confusing (
) with ( <x^2> ); remember that ( ) represents the average position while ( <x^2> ) is related to the spread or variance of the position. - Not considering the symmetry of cosine function, which can lead to incorrect evaluations of expected values.
AI-generated content may contain errors. Please verify critical information