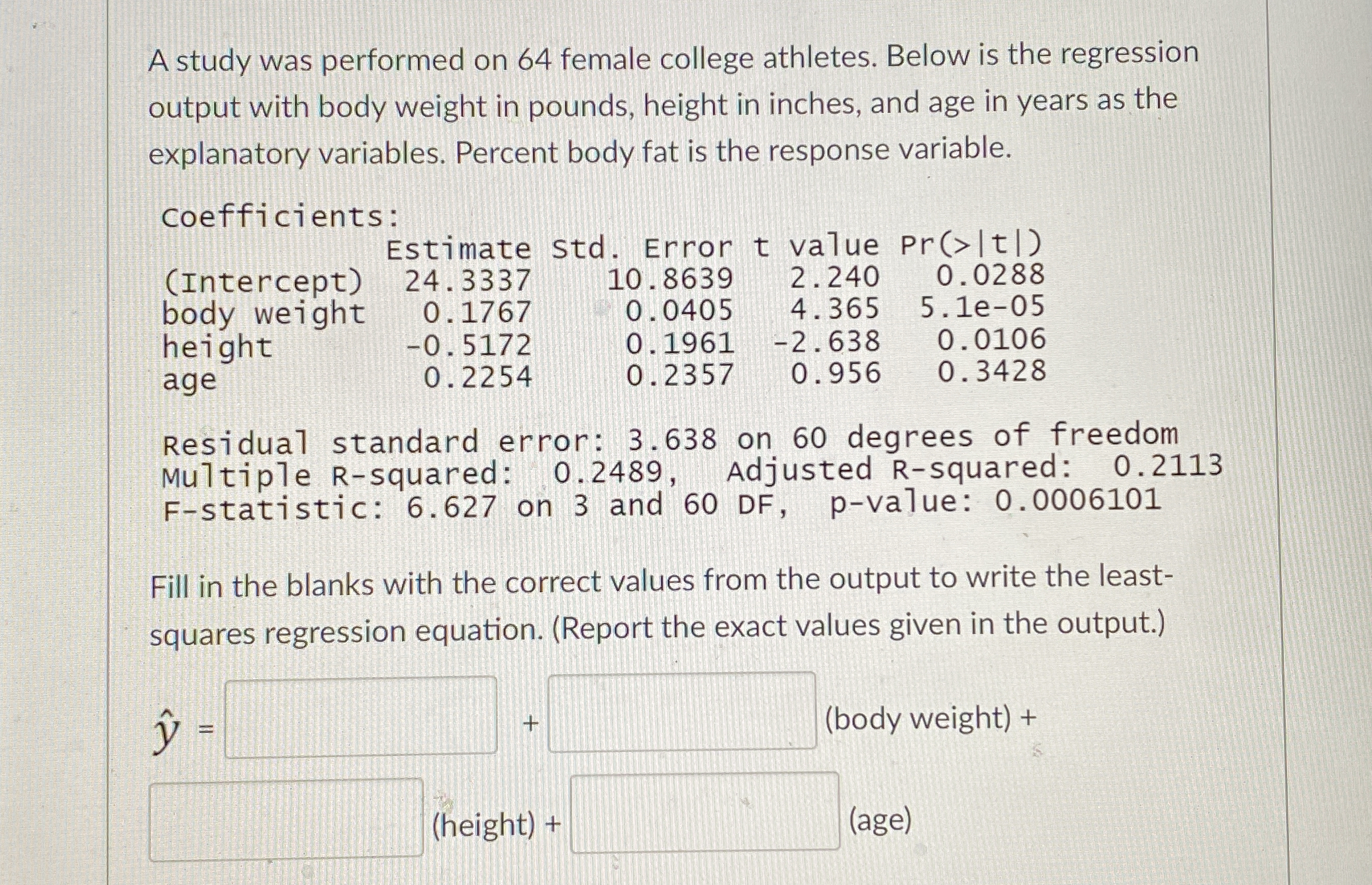
Fill in the blanks with the correct values from the output to write the least-squares regression equation. (Report the exact values given in the output.)
Understand the Problem
The question is asking for the completion of a least-squares regression equation using coefficients from a regression analysis output. The user needs to fill in specific values for the intercept, body weight, height, and age based on the provided coefficients.
Answer
$$ \hat{y} = 24.3337 + 0.1767 \cdot (\text{body weight}) - 0.5172 \cdot (\text{height}) + 0.2254 \cdot (\text{age}) $$
Answer for screen readers
$$ \hat{y} = 24.3337 + 0.1767 \cdot (\text{body weight}) - 0.5172 \cdot (\text{height}) + 0.2254 \cdot (\text{age}) $$
Steps to Solve
- Identify the coefficients from the regression output
From the provided coefficients, we have:
- Intercept: $24.3337$
- Body weight: $0.1767$
- Height: $-0.5172$
- Age: $0.2254$
- Formulate the regression equation
The general form of a least-squares regression equation is: $$ \hat{y} = \text{Intercept} + (\text{Coefficient for body weight}) \times (\text{body weight}) + (\text{Coefficient for height}) \times (\text{height}) + (\text{Coefficient for age}) \times (\text{age}) $$
- Substitute the coefficients into the equation
Plugging in the coefficients from step 1, the specific equation becomes: $$ \hat{y} = 24.3337 + 0.1767 \cdot (\text{body weight}) - 0.5172 \cdot (\text{height}) + 0.2254 \cdot (\text{age}) $$
This fills in the equation with the correct values.
$$ \hat{y} = 24.3337 + 0.1767 \cdot (\text{body weight}) - 0.5172 \cdot (\text{height}) + 0.2254 \cdot (\text{age}) $$
More Information
The least-squares regression equation provides a mathematical relationship between the percentage of body fat (the response variable) and the predictors: body weight, height, and age. The coefficients indicate how much the predicted value of body fat changes with a one-unit change in each predictor.
Tips
- Incorrectly signing coefficients: Be careful to note that height has a negative coefficient, meaning that an increase in height may reduce the predicted body fat.
- Omitting the intercept: The intercept is essential for completing the equation.
- Wrong variable placement: Ensure that each coefficient correlates with the respective variable in the equation correctly.
AI-generated content may contain errors. Please verify critical information