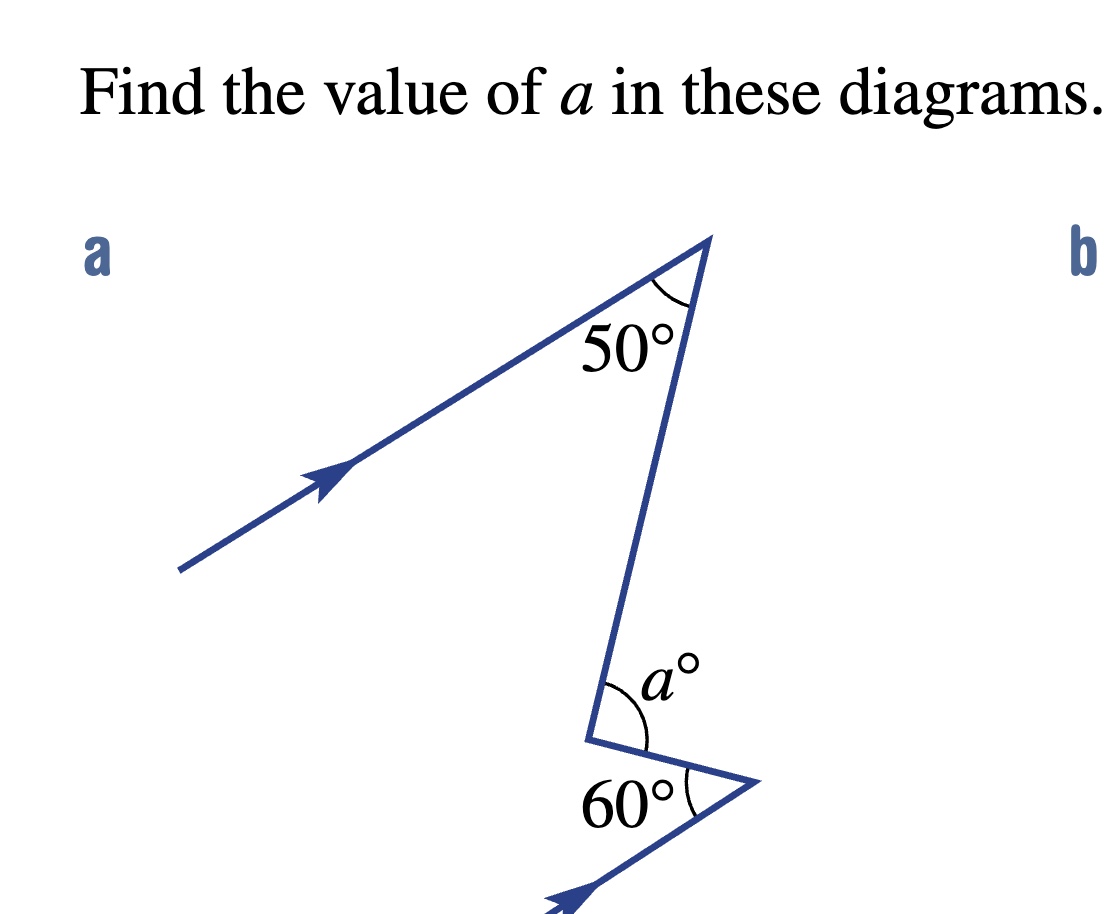
Find the value of a in these diagrams.
Understand the Problem
The question is asking to find the value of the angle 'a' in two diagrams provided. It involves understanding the properties of angles and potentially applying the concept of the sum of angles in a triangle or straight line.
Answer
The value of \( a \) in diagram a is \( 130^\circ \) and in diagram b is \( 120^\circ \).
Answer for screen readers
The value of ( a ) in diagram a is ( 130^\circ ) and in diagram b is ( 120^\circ ).
Steps to Solve
-
Understanding the Angle Relationships in Diagram a
In diagram a, we see that the angles involved include angle ( a ) and ( 50^\circ ). Since they are on a straight line, their sum must equal ( 180^\circ ): $$ a + 50^\circ = 180^\circ $$ -
Solve for angle a in Diagram a
Rearranging the equation from the first step gives us: $$ a = 180^\circ - 50^\circ $$
Calculating this gives: $$ a = 130^\circ $$ -
Understanding the Angle Relationships in Diagram b
In diagram b, we need to consider the angles ( a ), ( 60^\circ ), and the angle between the lines which also sums up to ( 180^\circ ): $$ a + 60^\circ + 180^\circ - a = 180^\circ $$
This simplifies to: $$ 60^\circ + a = 180^\circ $$ -
Solve for angle a in Diagram b
Rearranging the equation gives us: $$ a = 180^\circ - 60^\circ $$
Calculating this results in: $$ a = 120^\circ $$
The value of ( a ) in diagram a is ( 130^\circ ) and in diagram b is ( 120^\circ ).
More Information
The angles in both diagrams utilize the properties of supplementary angles, which state that angles summing up to ( 180^\circ ) are straight angles along a line.
Tips
- Forgetting that angles along a straight line must sum to ( 180^\circ ).
- Miscalculating the values during the subtraction step.
AI-generated content may contain errors. Please verify critical information