Expand (x² + 1/x²)^6
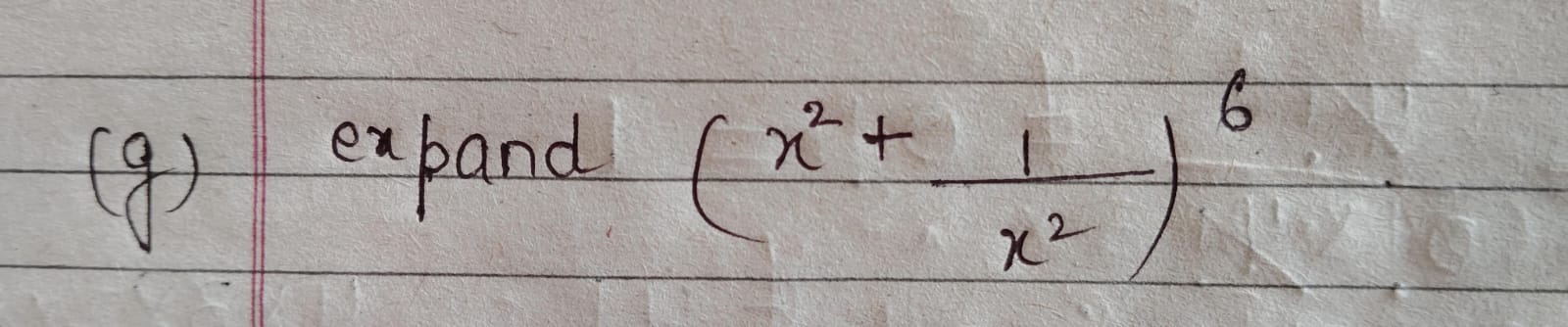
Understand the Problem
The question is asking to expand the expression (x² + rac{1}{x²})^6, which requires the use of the binomial theorem or polynomial expansion techniques.
Answer
The expanded expression is $$ x^{12} + 6x^{10} + 15x^8 + 20x^6 + 15x^4 + 6x^2 + 1 $$
Answer for screen readers
The expanded form of ( (x^2 + \frac{1}{x^2})^6 ) is:
$$ x^{12} + 6x^{10} + 15x^8 + 20x^6 + 15x^4 + 6x^2 + 1 $$
Steps to Solve
- Use the Binomial Theorem
The Binomial Theorem states that:
$$(a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k$$
In this case, let ( a = x^2 ) and ( b = \frac{1}{x^2} ), and ( n = 6 ).
- Apply the Binomial Theorem
We need to expand:
$$(x^2 + \frac{1}{x^2})^6 = \sum_{k=0}^{6} \binom{6}{k} (x^2)^{6-k} \left(\frac{1}{x^2}\right)^k$$
- Simplify the Terms
For each term in the expansion, simplify:
$$\binom{6}{k} (x^2)^{6-k} \left(\frac{1}{x^2}\right)^k = \binom{6}{k} x^{2(6-k)} x^{-2k} = \binom{6}{k} x^{12 - 2k}$$
So, we have:
$$(x^2 + \frac{1}{x^2})^6 = \sum_{k=0}^{6} \binom{6}{k} x^{12 - 2k}$$
- Calculate Each Coefficient
The value of ( \binom{6}{k} ) for ( k = 0, 1, 2, ..., 6 ):
- ( k = 0: \ \binom{6}{0} = 1 ) leading to ( x^{12} )
- ( k = 1: \ \binom{6}{1} = 6 ) leading to ( 6x^{10} )
- ( k = 2: \ \binom{6}{2} = 15 ) leading to ( 15x^8 )
- ( k = 3: \ \binom{6}{3} = 20 ) leading to ( 20x^6 )
- ( k = 4: \ \binom{6}{4} = 15 ) leading to ( 15x^4 )
- ( k = 5: \ \binom{6}{5} = 6 ) leading to ( 6x^2 )
- ( k = 6: \ \binom{6}{6} = 1 ) leading to ( 1 )
- Combine All Terms
Combining all terms gives us:
$$ (x^2 + \frac{1}{x^2})^6 = x^{12} + 6x^{10} + 15x^8 + 20x^6 + 15x^4 + 6x^2 + 1 $$
The expanded form of ( (x^2 + \frac{1}{x^2})^6 ) is:
$$ x^{12} + 6x^{10} + 15x^8 + 20x^6 + 15x^4 + 6x^2 + 1 $$
More Information
This expansion illustrates the application of the Binomial Theorem, which simplifies the calculations for polynomial expressions raised to a power. Each coefficient corresponds to a different combination of the terms from the original expression.
Tips
- Forgetting the binomial coefficients: Some might omit the coefficients from the Binomial Theorem while expanding.
- Incorrectly calculating powers: Ensure the powers are correctly calculated based on ( (x^2) ) and ( \frac{1}{x^2} ).
- Misplacing terms: Double-check the arrangement of terms to ensure all are included.
AI-generated content may contain errors. Please verify critical information