Expand the expression to a polynomial in standard form: (2x - 1)(2x^2 - x + 7)
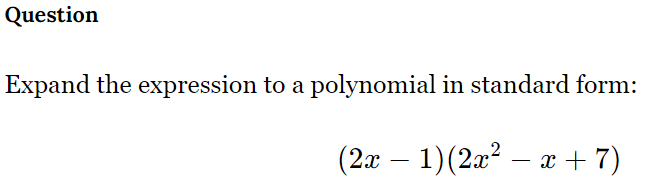
Understand the Problem
The question is asking us to expand the given expression, which consists of two polynomials, into a single polynomial in standard form. This involves using the distributive property or FOIL method to combine like terms.
Answer
The expanded polynomial is $4x^3 - 4x^2 + 15x - 7$.
Answer for screen readers
The expanded polynomial in standard form is: $$ 4x^3 - 4x^2 + 15x - 7 $$
Steps to Solve
-
Use the distributive property Begin by distributing each term of the first polynomial ( (2x - 1) ) to every term in the second polynomial ( (2x^2 - x + 7) ).
-
First distribution Distribute ( 2x ) to each term in ( (2x^2 - x + 7) ): [ 2x \cdot 2x^2 = 4x^3 ] [ 2x \cdot (-x) = -2x^2 ] [ 2x \cdot 7 = 14x ]
-
Second distribution Now distribute ( -1 ) to each term in ( (2x^2 - x + 7) ): [ -1 \cdot 2x^2 = -2x^2 ] [ -1 \cdot (-x) = x ] [ -1 \cdot 7 = -7 ]
-
Combine all terms Now combine all the results from the distributions: [ 4x^3 + (-2x^2) + 14x + (-2x^2) + x - 7 ]
-
Combine like terms Combine the like terms:
- The ( x^2 ) terms: ( -2x^2 - 2x^2 = -4x^2 )
- The ( x ) terms: ( 14x + x = 15x )
Thus, the expression combines to: [ 4x^3 - 4x^2 + 15x - 7 ]
The expanded polynomial in standard form is: $$ 4x^3 - 4x^2 + 15x - 7 $$
More Information
The expansion of polynomials is an essential skill in algebra, allowing you to simplify expressions for further analysis or calculations. When multiplying polynomials, remember to carefully distribute each term and combine like terms systematically.
Tips
- Forgetting to distribute each term to all terms in the other polynomial.
- Not combining like terms correctly, leading to incorrect coefficients.