Examine the differentiability of the following function: f(x) = { x^2 sin(1/x), x ≠ 0; 0, x = 0 } at x = 0.
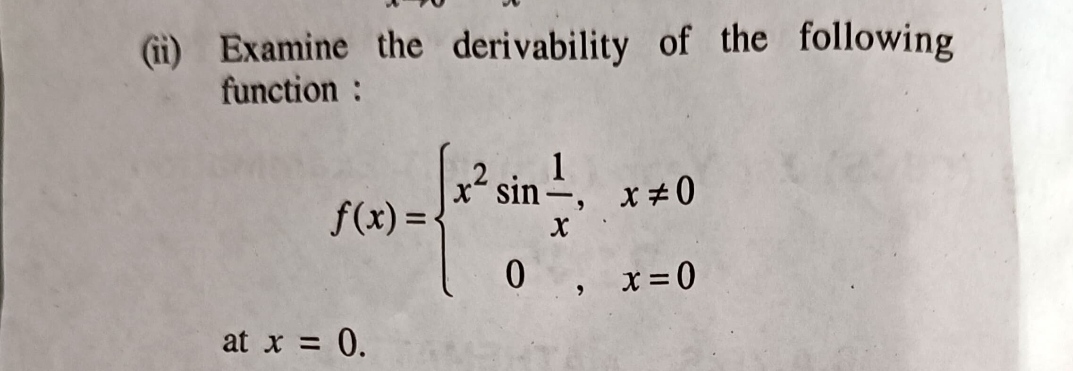
Understand the Problem
The question is asking for an examination of the differentiability of the given piecewise function at the point x = 0. This involves checking if the derivative exists at that point by evaluating the function and its limit as x approaches 0.
Answer
The function is differentiable at $x = 0$ with $f'(0) = 0$.
Answer for screen readers
The function $f(x)$ is differentiable at $x = 0$, with $f'(0) = 0$.
Steps to Solve
-
Function Definition and Continuity Check To check differentiability, we first need the function to be continuous at $x = 0$. The function is defined as: $$ f(x) = \begin{cases} x^2 \sin\left(\frac{1}{x}\right) & \text{if } x \neq 0 \ 0 & \text{if } x = 0 \end{cases} $$ To check continuity at $x = 0$, we calculate: $$ \lim_{x \to 0} f(x) = \lim_{x \to 0} x^2 \sin\left(\frac{1}{x}\right) $$ Since $|\sin\left(\frac{1}{x}\right)| \leq 1$, we have: $$ |f(x)| \leq |x^2| \rightarrow 0 \text{ as } x \to 0 \Rightarrow f(0) = 0 $$ Thus, $f(x)$ is continuous at $x = 0$.
-
Checking the Derivative at $x = 0$ Next, we need to evaluate the derivative of $f(x)$ at $x = 0$ using the limit definition of the derivative: $$ f'(0) = \lim_{h \to 0} \frac{f(h) - f(0)}{h} = \lim_{h \to 0} \frac{f(h)}{h} = \lim_{h \to 0} \frac{h^2 \sin\left(\frac{1}{h}\right)}{h} $$ This simplifies to: $$ \lim_{h \to 0} h \sin\left(\frac{1}{h}\right) $$
-
Limit Evaluation The term $h \sin\left(\frac{1}{h}\right)$ oscillates between $-h$ and $h$: $$ -h \leq h \sin\left(\frac{1}{h}\right) \leq h $$ As $h \to 0$, both bounds approach $0$.
-
Final Derivative Result Thus, using the Squeeze Theorem: $$ \lim_{h \to 0} h \sin\left(\frac{1}{h}\right) = 0 $$ Therefore, $f'(0) = 0$.
The function $f(x)$ is differentiable at $x = 0$, with $f'(0) = 0$.
More Information
This piecewise function is continuous and differentiable at the point $x = 0$. The fact that $f'(0) = 0$ shows that the tangent at that point is horizontal.
Tips
- Not checking continuity first: Always ensure the function is continuous at the point of interest before checking differentiability.
- Forgetting the limit form of the derivative: The definition of the derivative at a point is crucial; missing this step can lead to incorrect conclusions.