Evaluate the integral of (3√(1 + 4√x) / √x) dx.
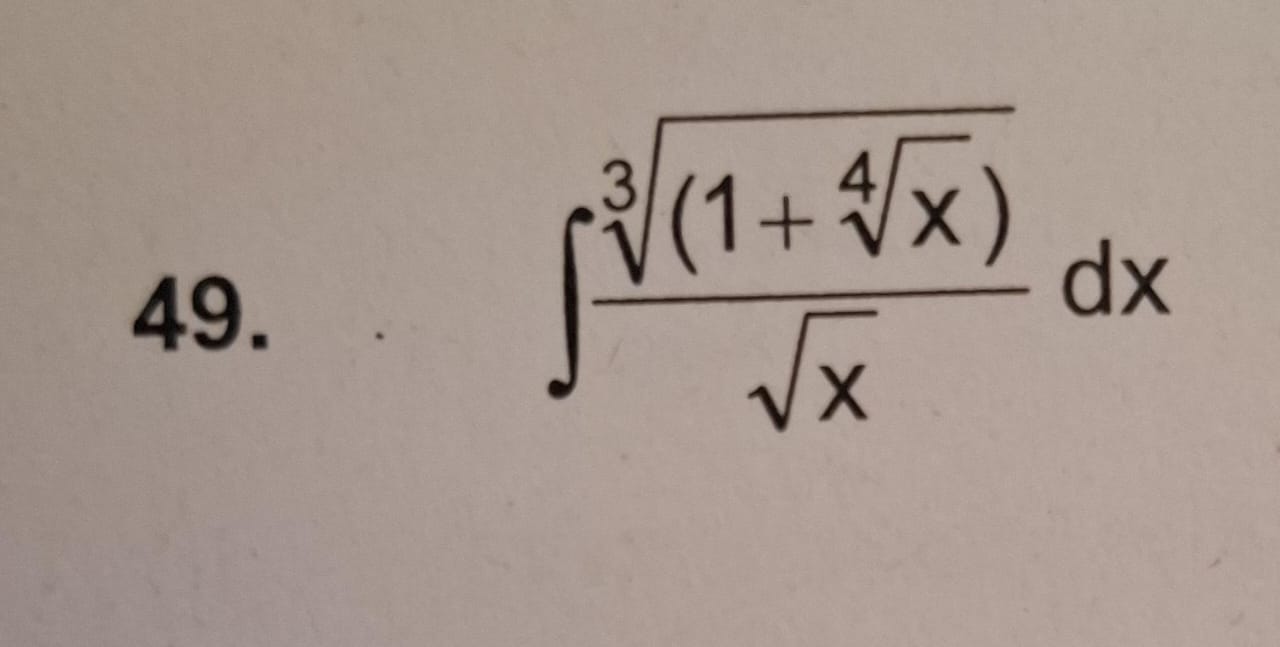
Understand the Problem
The question requires evaluating the integral of a complex function involving square roots and a variable x. We will approach this by using techniques of integration, possibly including substitution or integration by parts.
Answer
The integral evaluates to $ (1 + 4\sqrt{x})^{3/2} + C $
Answer for screen readers
The final answer is
$$ (1 + 4\sqrt{x})^{3/2} + C $$
Steps to Solve
- Rewrite the Integral We express the integral in a simpler form. The given integral is
$$ \int \frac{3\sqrt{(1 + 4\sqrt{x})}}{\sqrt{x}} , dx $$
This can be rewritten as:
$$ 3 \int \frac{\sqrt{1 + 4\sqrt{x}}}{\sqrt{x}} , dx $$
- Substitute for Simplicity Let’s substitute $u = \sqrt{x}$, which means that $x = u^2$ and $dx = 2u , du$. Then, the integral transforms to:
$$ 3 \int \frac{\sqrt{1 + 4u}}{u} \cdot (2u) , du $$
This simplifies to:
$$ 6 \int (1 + 4u)^{1/2} , du $$
- Expand the Integral Next, we can break this integral down using the binomial expansion:
$$ 6 \int (1 + 4u)^{1/2} , du = 6 \int (1 + 4u)^{1/2} , du $$
Using the substitution method: Let $v = 1 + 4u$, then $dv = 4,du \Rightarrow du = \frac{1}{4}dv$.
- Integral Transformation Substituting gives us:
$$ 6 \cdot \frac{1}{4} \int v^{1/2} , dv = \frac{3}{2} \int v^{1/2} , dv $$
- Integrate Now, we can integrate $v^{1/2}$:
$$ \frac{3}{2} \cdot \frac{2}{3} v^{3/2} + C = v^{3/2} + C $$
Substituting back $v = 1 + 4u$ gives:
$$ (1 + 4u)^{3/2} + C $$
- Re-substitute for x Finally, we replace $u$ back with $\sqrt{x}$:
$$ (1 + 4\sqrt{x})^{3/2} + C $$
Thus, the final answer for the integral is:
$$ \int \frac{3\sqrt{(1 + 4\sqrt{x})}}{\sqrt{x}} , dx = (1 + 4\sqrt{x})^{3/2} + C $$
The final answer is
$$ (1 + 4\sqrt{x})^{3/2} + C $$
More Information
This integral showcases the utility of substitution methods in calculus, allowing for complex functions to be simplified into more manageable forms. Such techniques are crucial for solving higher-order integrals efficiently.
Tips
- Neglecting Substitution: Forgetting to substitute back to the original variable.
- Sign Errors: Mismanagement of signs, particularly when dealing with terms involving square roots.
- Incorrect Integral Handling: Failing to perform the integral step correctly after substitution.
AI-generated content may contain errors. Please verify critical information