Evaluate the integral \( \int \frac{x^2 + 4x^3 + 2}{6x} \, dx \)
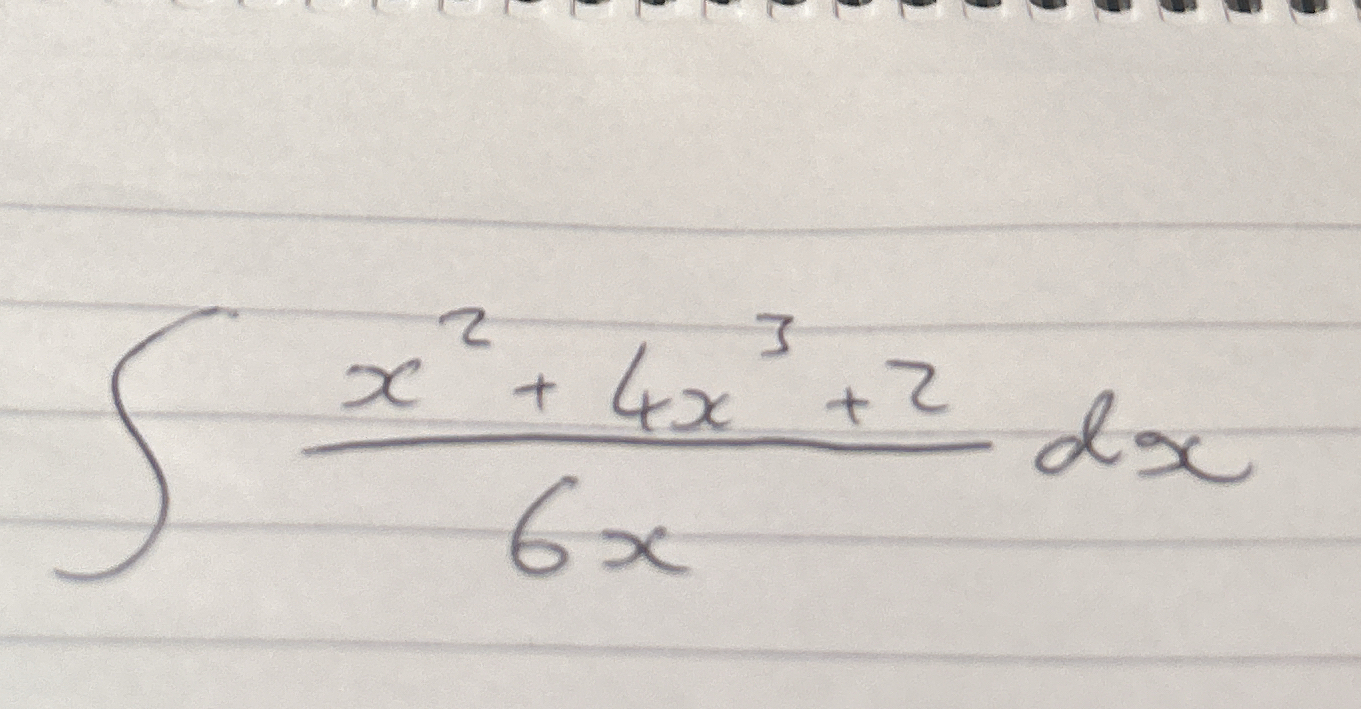
Understand the Problem
The question is asking for the evaluation of the integral of a polynomial expression in terms of x, specifically [ \int \frac{x^2 + 4x^3 + 2}{6x} , dx ]. This can be solved using integration techniques for rational functions.
Answer
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C $$
Answer for screen readers
The evaluated integral is
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C. $$
Steps to Solve
- Simplify the Integral
We can simplify the integrand before integrating. The expression inside the integral is
$$ \frac{x^2 + 4x^3 + 2}{6x}. $$
Divide each term by ( 6x ):
$$ \frac{x^2}{6x} + \frac{4x^3}{6x} + \frac{2}{6x} = \frac{x}{6} + \frac{2}{3}x^2 + \frac{1}{3x}. $$
Thus, our integral becomes:
$$ \int \left( \frac{x}{6} + \frac{2}{3}x^2 + \frac{1}{3x} \right) dx. $$
- Integrate Each Term
Now we can integrate each term separately:
- The integral of ( \frac{x}{6} ) is:
$$ \int \frac{x}{6} , dx = \frac{1}{6} \cdot \frac{x^2}{2} = \frac{x^2}{12}. $$
- The integral of ( \frac{2}{3} x^2 ) is:
$$ \int \frac{2}{3} x^2 , dx = \frac{2}{3} \cdot \frac{x^3}{3} = \frac{2x^3}{9}. $$
- The integral of ( \frac{1}{3x} ) is:
$$ \int \frac{1}{3x} , dx = \frac{1}{3} \ln |x|. $$
Combine these results:
$$ \int \left( \frac{x}{6} + \frac{2}{3}x^2 + \frac{1}{3x} \right) dx = \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C. $$
- Write the Final Answer
The final answer, combining all terms and adding a constant of integration ( C ), is:
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C. $$
The evaluated integral is
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C. $$
More Information
The result of this integration can be useful in applications involving areas under curves represented by polynomial functions. The logarithmic term reflects the behavior of the function as ( x ) approaches zero, demonstrating the importance of limits in calculus.
Tips
- Forgetting to include the constant of integration ( C ) at the end.
- Failing to simplify the integrand correctly before integrating.
- Mixing up the coefficients when integrating; double-check that each term is handled properly.
AI-generated content may contain errors. Please verify critical information