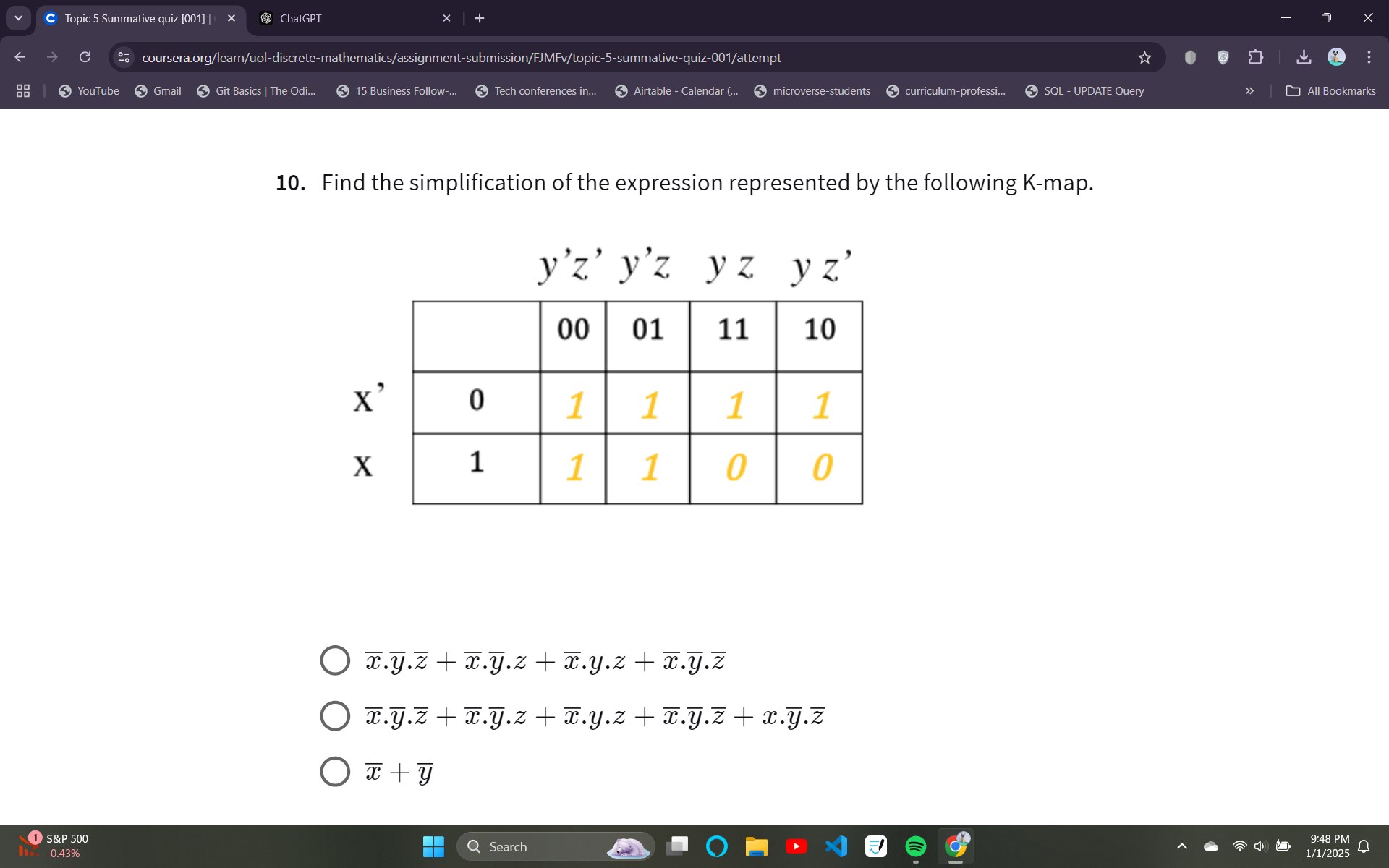
Find the simplification of the expression represented by the following K-map.

Steps to Solve

1. Understand the K-map layout

   The K-map given is organized for three variables (X, Y, Z). The first variable (X) is represented in rows, and the others are on the columns. The K-map has the following values:

   • Row $X' (0)$: Columns $00$ (1), $01$ (1), $11$ (1), $10$ (1)
   • Row $X (1)$: Columns $00$ (1), $01$ (1), $11$ (0), $10$ (0)

2. Identify the minterms

   The K-map has $1$s in the following positions:

   • $X'Y'Z'$ (cell $00$)
   • $X'Y'Z$ (cell $01$)
   • $X'YZ$ (cell $11$)
   • $X'YZ'$ (cell $10$)
   • $XY'Z'$ (cell $00$)
   • $XY'Z$ (cell $01$)

   This can be translated to minterms:

   • From row $X' (0)$: $X'Y'Z'$, $X'Y'Z$, $X'YZ$, $X'YZ'$
   • From row $X (1)$: $XY'Z'$, $XY'Z$

3. Group adjacent 1s

   A K-map allows grouping $1$s together:

   • Group the four $1$s from row $X' (0)$:
     • $X'Y'$ (covers $Y'Z'$ and $Y'Z$)
   • Group the two $1$s from row $X (1)$:
     • $XY'$ (covers $Y'Z'$ and $Y'Z$)

4. Write the simplified expression

   From the groups, we derive the simplified expression:

   • First group: $X'Y'$
   • Second group: $XY'$

   Thus, the overall simplified expression is: $$ X'Y' + XY' $$