Evaluate the integral ∫(1 + 3x)x² dx.

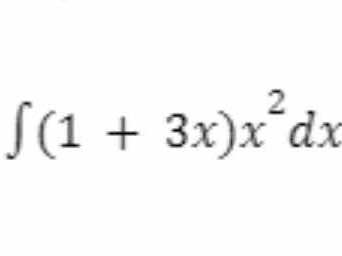
Understand the Problem

The question is asking for the evaluation of the integral of the expression (1 + 3x)x² with respect to x.

Answer

$$\frac{x^3}{3} + \frac{3x^4}{4} + C$$

Steps to Solve

Expand the integrand
First, we will expand the expression ( (1 + 3x)x^2 ) before integrating.
Using the distributive property:
$$(1 + 3x)x^2 = x^2 + 3x^3$$
Set up the integral
Now, the integral can be rewritten as:
$$\int (1 + 3x)x^2 , dx = \int (x^2 + 3x^3) , dx$$
Integrate term by term
Next, we integrate each term separately:

The integral of ( x^2 ) is given by:
$$\int x^2 , dx = \frac{x^{3}}{3}$$
The integral of ( 3x^3 ) is given by:
$$\int 3x^3 , dx = 3 \cdot \frac{x^{4}}{4} = \frac{3x^{4}}{4}$$

Combine the results
Now, combine the results from the previous step:
$$\int (x^2 + 3x^3) , dx = \frac{x^3}{3} + \frac{3x^4}{4} + C$$
where ( C ) is the constant of integration.

The final answer is:
$$\frac{x^3}{3} + \frac{3x^4}{4} + C$$

More Information

This integral combines basic techniques of algebra and integration. The process of expanding the polynomial before integration is a common technique that simplifies calculations, enabling easier evaluation term by term.

Tips

Forgetting to add the constant of integration ( C ) when evaluating indefinite integrals. Always remember to include it.
Not expanding the polynomial correctly, which can lead to errors in the individual integrations.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!