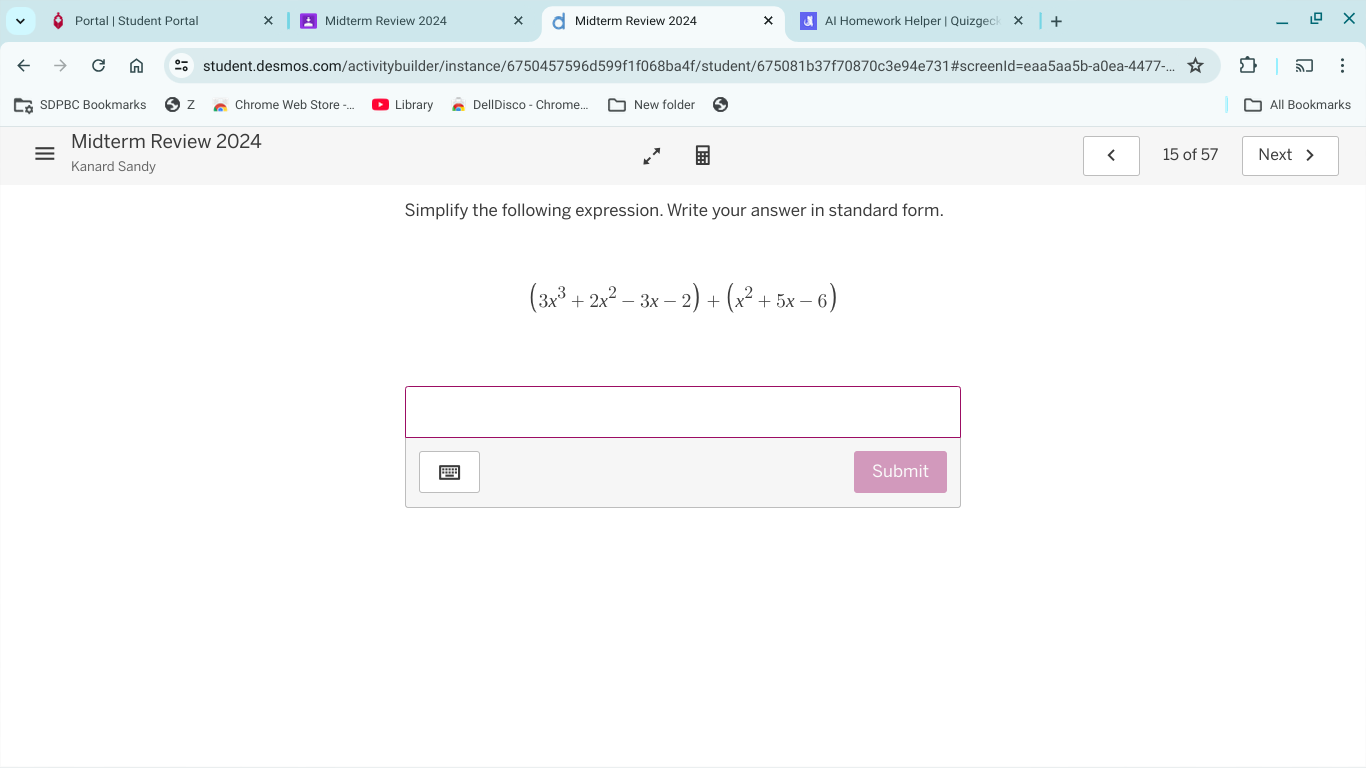
Simplify the following expression. Write your answer in standard form: (3x³ + 2x² - 3x - 2) + (x² + 5x - 6)
Understand the Problem
The question is asking to simplify the given algebraic expression and write the answer in standard form. This involves combining like terms and organizing the expression properly.
Answer
$$3x^3 + 3x^2 + 2x - 8$$
Answer for screen readers
The simplified expression in standard form is:
$$3x^3 + 3x^2 + 2x - 8$$
Steps to Solve
- Combine the expressions inside the parentheses
We have the expression: $$(3x^3 + 2x^2 - 3x - 2) + (x^2 + 5x - 6)$$
First, we can remove the parentheses as they don't affect the addition:
$$3x^3 + 2x^2 - 3x - 2 + x^2 + 5x - 6$$
- Group like terms
Now we group similar terms together:
- For $x^3$: (3x^3)
- For $x^2$: (2x^2 + x^2 = 3x^2)
- For $x$: (-3x + 5x = 2x)
- For the constant terms: (-2 - 6 = -8)
- Write the simplified expression
Now combining these results, we get:
$$3x^3 + 3x^2 + 2x - 8$$
This is the final expression in standard form.
The simplified expression in standard form is:
$$3x^3 + 3x^2 + 2x - 8$$
More Information
The expression represents a cubic polynomial, and the standard form organizes the terms from highest to lowest degree. Cubic functions can have interesting properties, like having up to three real roots.
Tips
- Forgetting to combine like terms properly.
- Neglecting the negative signs when subtracting constant terms.
- Writing the polynomial in an unordered manner instead of in standard form.
AI-generated content may contain errors. Please verify critical information