Evaluate lim x->1 (x^2 - x) / (x - 1 - log(x))
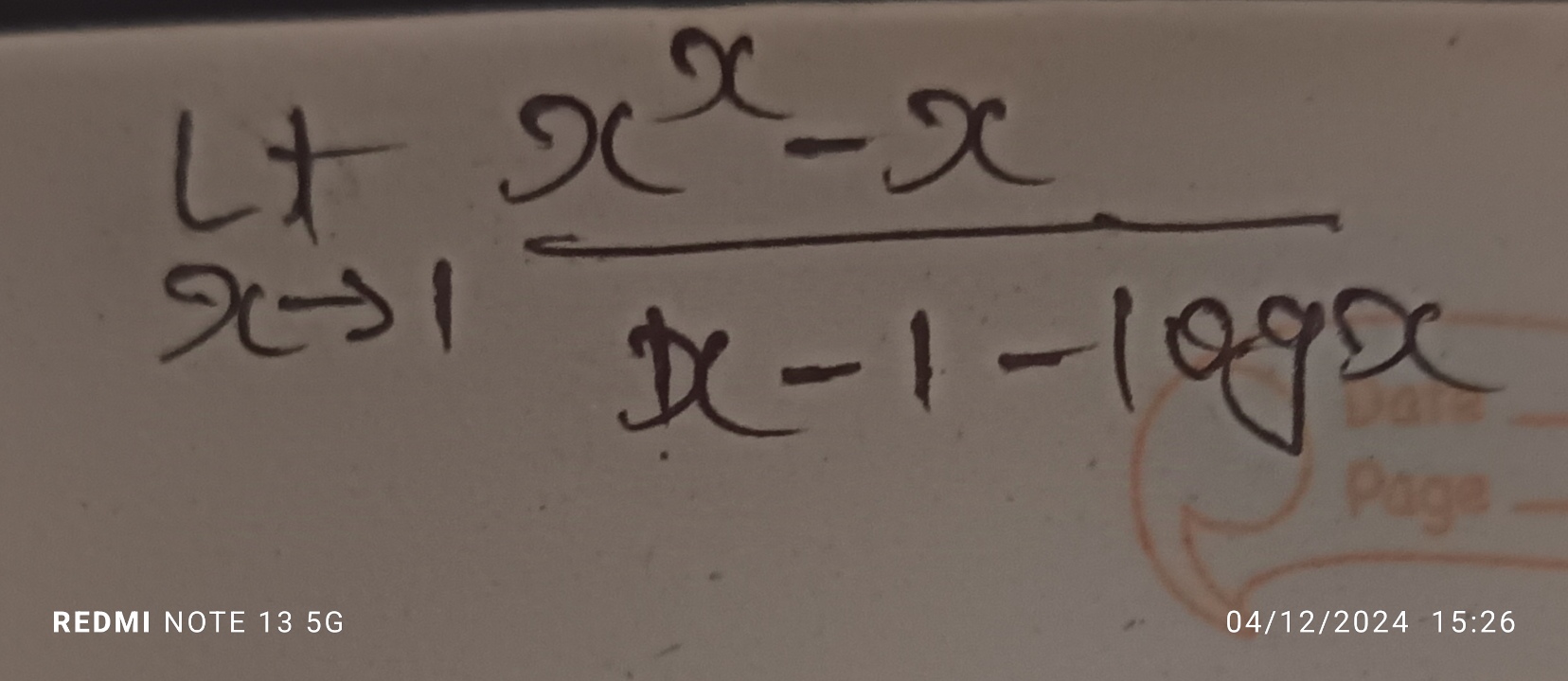
Understand the Problem
The question involves evaluating the limit as x approaches 1 of the expression (x^2 - x) / (x - 1 - log(x)). It requires understanding the concepts of limits and derivatives.
Answer
The limit is $2$.
Answer for screen readers
The limit is $2$.
Steps to Solve
- Substituting x = 1
Start by substituting $x = 1$ into the expression to check for an indeterminate form:
$$ \frac{(1^2 - 1)}{(1 - 1 - \log(1)) = \frac{0}{0} $$
Since this results in the form $\frac{0}{0}$, we need to use L'Hôpital's rule.
- Applying L'Hôpital's Rule
Differentiate the numerator and the denominator separately:
- The derivative of the numerator ($x^2 - x$) is $2x - 1$.
- The derivative of the denominator ($x - 1 - \log(x)$) is $1 - \frac{1}{x}$.
Now we can rewrite the limit as:
$$ \lim_{x \to 1} \frac{2x - 1}{1 - \frac{1}{x}} $$
- Finding the new limit
Substitute $x = 1$ into the new expression:
$$ \frac{2(1) - 1}{1 - 1} = \frac{1}{0} $$
This is undefined, so we need to analyze the limit further.
- Further Applying L'Hôpital's Rule
Since we again have an indeterminate form, apply L'Hôpital's rule once more. Differentiate the numerator and denominator again:
- The derivative of the numerator ($2x - 1$) is $2$.
- The derivative of the denominator ($1 - \frac{1}{x}$) is $\frac{1}{x^2}$.
Now we have:
$$ \lim_{x \to 1} \frac{2}{\frac{1}{x^2}} = \lim_{x \to 1} 2x^2 = 2(1^2) = 2 $$
- Conclusion
The limit as $x$ approaches 1 is $2$.
The limit is $2$.
More Information
L'Hôpital's rule is a powerful tool for evaluating limits that result in indeterminate forms such as $\frac{0}{0}$ or $\frac{\infty}{\infty}$. By repeatedly differentiating, we can often find a limit that is easier to evaluate.
Tips
- Forgetting to apply L'Hôpital's rule correctly; it's important to differentiate both the numerator and denominator.
- Not recognizing when the expression still leads to an indeterminate form after the first application of L'Hôpital's rule.
AI-generated content may contain errors. Please verify critical information