Evaluate ∫(from a to b) (log x)/x dx.

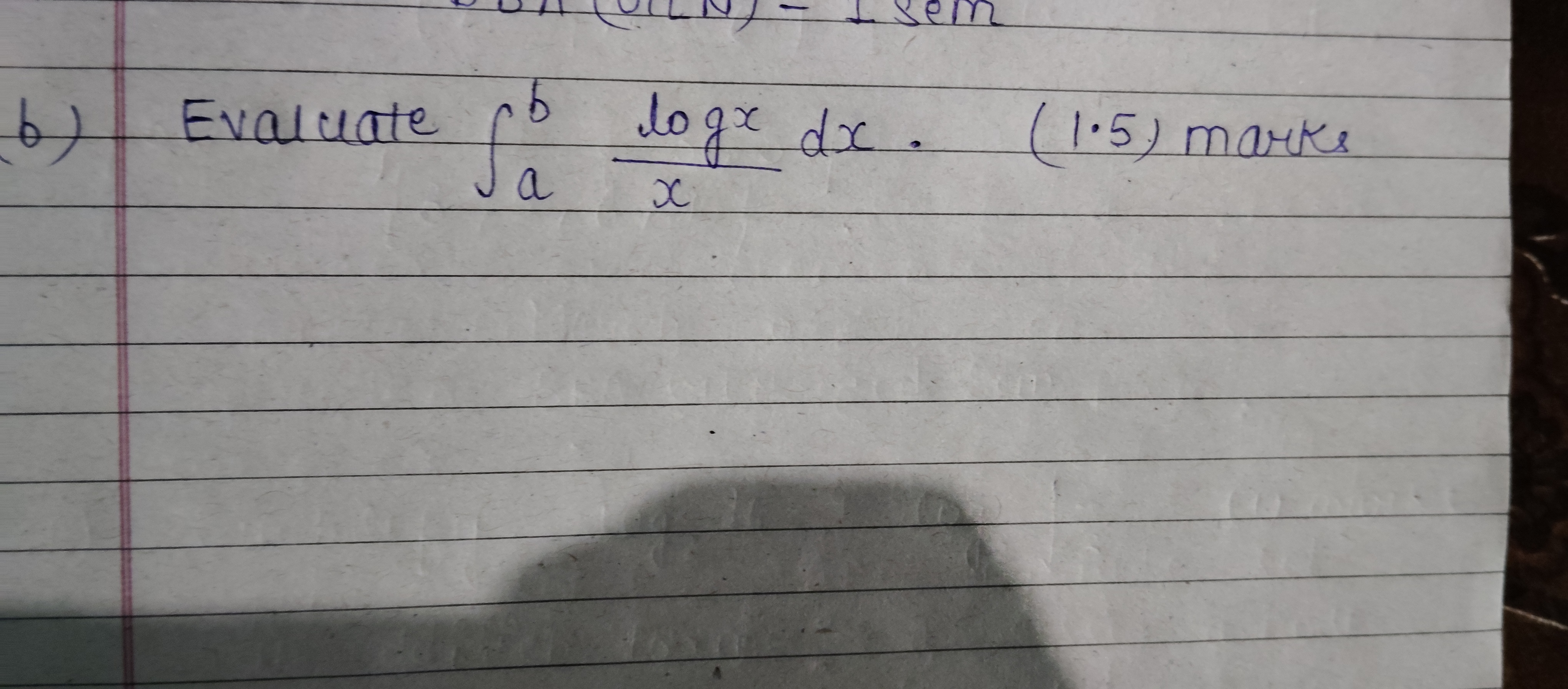
Understand the Problem

The question is asking to evaluate the definite integral of the function log(x)/x from a to b, indicating a need for integration techniques.

Answer

$$ I = -\frac{\log b}{b} + \frac{1}{b} + \frac{\log a}{a} - \frac{1}{a} $$

Steps to Solve

Identify the integral to evaluate

We need to evaluate the definite integral: $$ \int_{a}^{b} \frac{\log x}{x} , dx $$

Use a substitution method

Let ( u = \log x ). Then, the derivative of ( u ) gives: $$ \frac{du}{dx} = \frac{1}{x} \implies dx = x , du = e^u , du $$ Substituting ( x = e^u ) makes the integral become: $$ \int \frac{u}{e^u} , du $$

Solve the integral using integration by parts

Using integration by parts, where:

Let ( v = u ) and ( dw = e^{-u} , du )
Then ( dv = du ) and ( w = -e^{-u} )

The formula for integration by parts is: $$ \int v , dw = vw - \int w , dv $$

Applying this, we have: $$ \int u e^{-u} , du = -u e^{-u} - \int -e^{-u} , du $$ So, $$ = -u e^{-u} + e^{-u} + C $$

Substituting back to ( x )

Now, revert ( u ) back to ( \log x ): $$ = -(\log x) \frac{1}{x} + \frac{1}{x} + C $$

Evaluate the definite integral from ( a ) to ( b )

Now, evaluate at the limits ( a ) and ( b ): $$ I = \left[ -\frac{\log x}{x} + \frac{1}{x} \right]_{a}^{b} $$

Calculating gives: $$ I = \left( -\frac{\log b}{b} + \frac{1}{b} \right) - \left( -\frac{\log a}{a} + \frac{1}{a} \right) $$

The final answer is: $$ I = -\frac{\log b}{b} + \frac{1}{b} + \frac{\log a}{a} - \frac{1}{a} $$

More Information

This type of integral often appears in calculus, especially related to problems involving logarithmic functions. The integral of ( \frac{\log x}{x} ) is closely related to the gamma and digamma functions in advanced mathematics.

Tips

Forgetting to change the limits of integration after substitution.
Not applying integration by parts correctly, especially handling constants.
Confusing ( u = \log x ) with ( x = e^u ).

Thank you for voting!