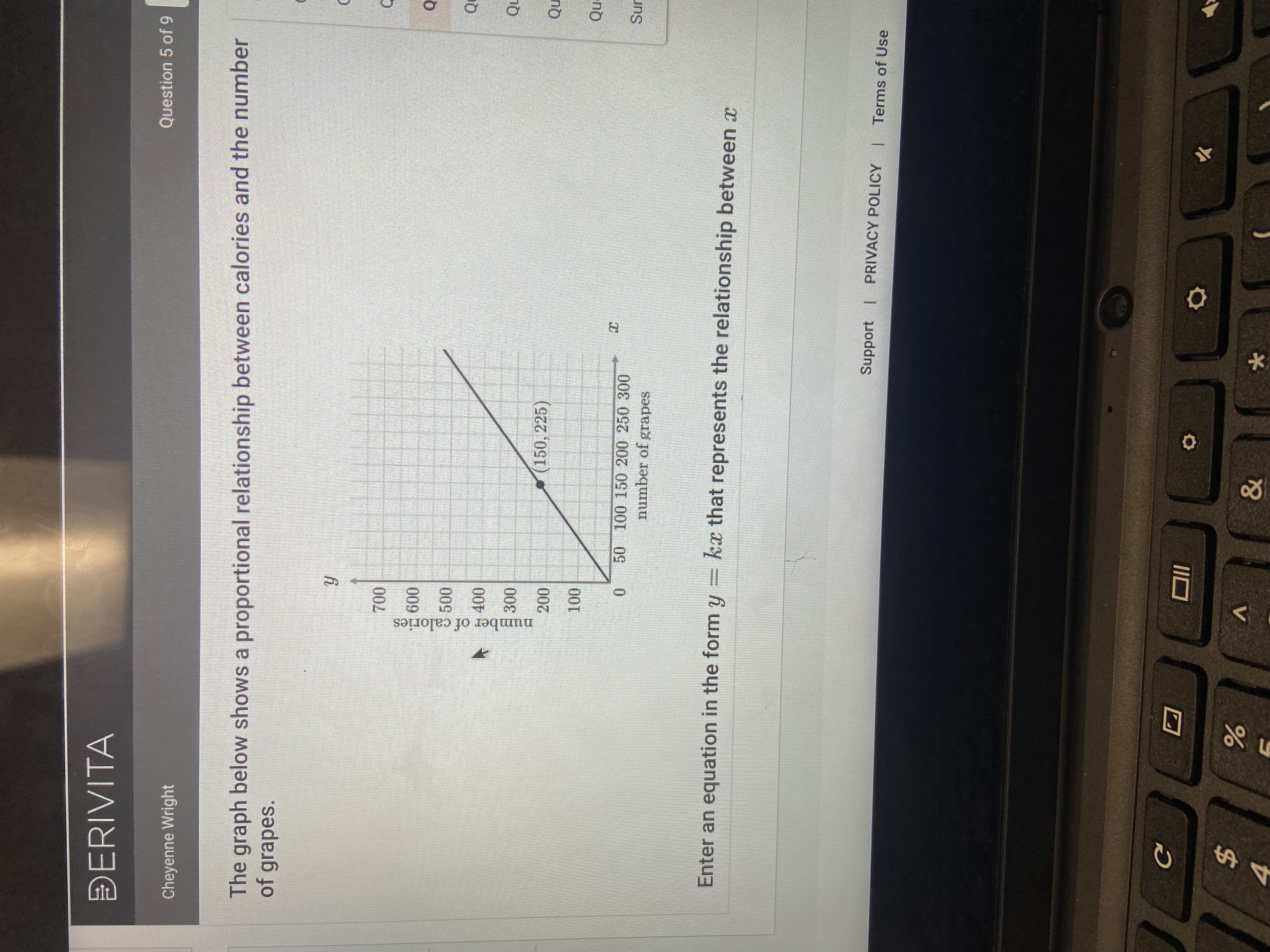
Enter an equation in the form y = kx that represents the relationship between x and y.

Understand the Problem

The question is asking to determine the equation of a proportional relationship between the number of calories (y) and the number of grapes (x) based on the information given in the graph.

Answer

The equation is $ y = \frac{3}{2}x $.

Steps to Solve

Identify the point on the graph The graph shows the point $(150, 225)$, meaning that for 150 grapes, there are 225 calories. This point will be used to find the proportionality constant.
Determine the proportionality constant The proportional relationship can be expressed as $y = kx$, where $k$ is the proportionality constant. Using the point identified: $$ k = \frac{y}{x} = \frac{225}{150} $$
Calculate the value of k Now, simplify the fraction to find the value of $k$: $$ k = \frac{225 \div 75}{150 \div 75} = \frac{3}{2} $$
Write the equation Substituting the value of $k$ back into the relationship gives us: $$ y = \frac{3}{2}x $$

The equation representing the relationship is ( y = \frac{3}{2}x ).

More Information

This equation shows that for every grape consumed, the calories increase by 1.5 times, indicating a direct proportional relationship between the number of grapes and calories.

Tips

Forgetting to simplify the fraction when calculating ( k ).
Not recognizing that the point given on the graph corresponds to the values of ( x ) and ( y ) needed for the calculations.

Thank you for voting!