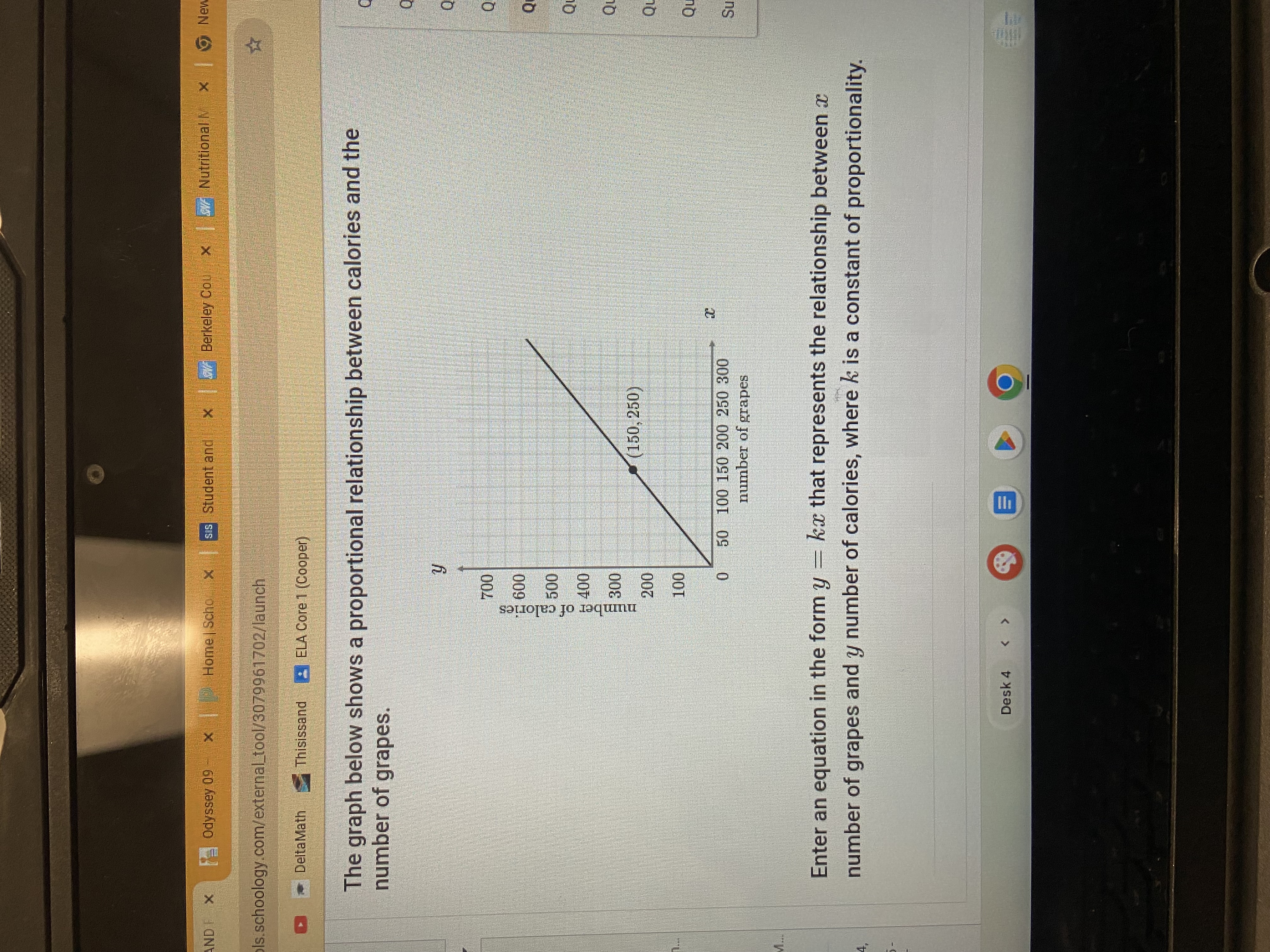
Enter an equation in the form y = kx that represents the relationship between the number of grapes and y number of calories, where k is a constant of proportionality.
Understand the Problem
The question is asking for an equation that represents the proportional relationship between the number of grapes (x) and the calories (y) based on the graph provided. We need to determine the constant of proportionality (k) and write the equation in the form y = kx.
Answer
The equation is \( y = \frac{5}{3}x \).
Answer for screen readers
The equation that represents the relationship is:
$$ y = \frac{5}{3}x $$
Steps to Solve
- Identify Known Points on the Graph
From the graph, we can identify a specific point, such as (150, 250). This means when there are 150 grapes (x), there are 250 calories (y).
- Calculate the Constant of Proportionality (k)
We can use the point (150, 250) to find the constant of proportionality. The relationship is given by the equation ( y = kx ).
Using the known values:
$$ 250 = k \times 150 $$
To solve for ( k ):
$$ k = \frac{250}{150} $$
- Simplify k
Now we simplify ( k ):
$$ k = \frac{250 \div 50}{150 \div 50} = \frac{5}{3} $$
- Write the Final Equation
Now that we have ( k ), we substitute it back into the equation ( y = kx ):
$$ y = \frac{5}{3}x $$
The equation that represents the relationship is:
$$ y = \frac{5}{3}x $$
More Information
This equation shows a linear relationship where the calories are proportional to the number of grapes. For every 3 grapes, there are approximately 5 calories.
Tips
- Forgetting to simplify ( k ): Always reduce fractions to their simplest form.
- Misreading coordinates: Ensure you correctly interpret points from the graph.
