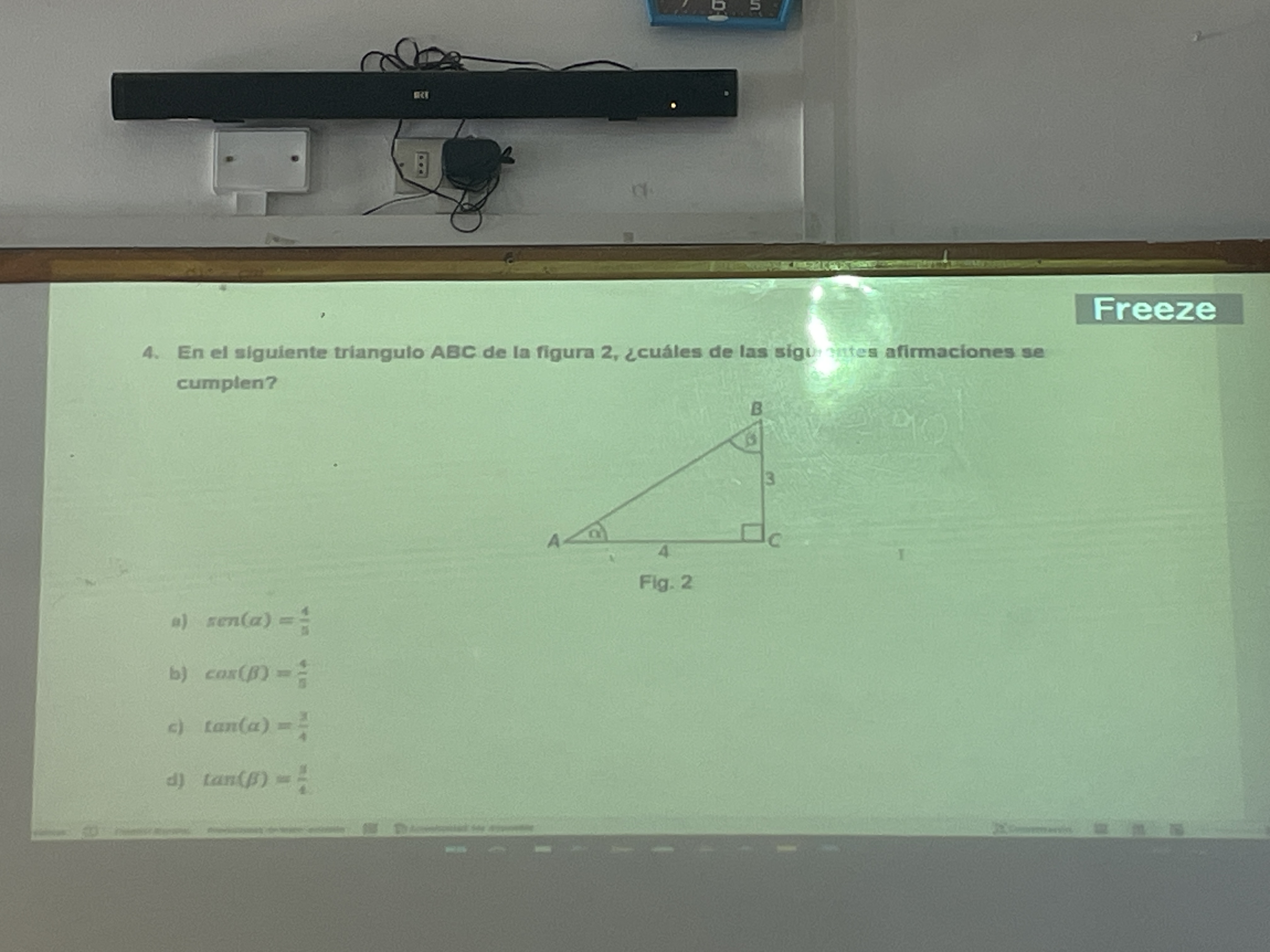
En el siguiente triángulo ABC de la figura 2, ¿cuáles de las siguientes afirmaciones se cumplen?
Understand the Problem
La pregunta se refiere a un triángulo ABC en el que se deben verificar ciertas afirmaciones relacionadas con las funciones trigonométricas basadas en el triángulo mostrado. Se busca identificar cuáles de las afirmaciones son correctas.
Answer
Las afirmaciones correctas son: - a) $\sin(A) = \frac{3}{5}$. - b) $\cos(B) = \frac{4}{5}$. - c) $\tan(A) = \frac{3}{4}$. - d) $\tan(B) = \frac{4}{3}$.
Answer for screen readers
Las afirmaciones correctas son:
- a) $\sin(A) = \frac{3}{5}$.
- b) $\cos(B) = \frac{4}{5}$.
- c) $\tan(A) = \frac{3}{4}$.
- d) $\tan(B) = \frac{4}{3}$.
Steps to Solve
- Identificación de lados en el triángulo
En el triángulo ABC, identificamos los lados. Con base en la figura, el lado opuesto al ángulo $A$ es $BC$ y su longitud es $3$. El lado adyacente a $A$ es $AC$ y su longitud es $4$. La hipotenusa es $AB$.
- Cálculo de la hipotenusa
Usamos el teorema de Pitágoras para encontrar la hipotenusa $AB$:
$$ AB = \sqrt{(AC^2 + BC^2)} = \sqrt{(4^2 + 3^2)} = \sqrt{16 + 9} = \sqrt{25} = 5. $$
- Cálculo de las funciones trigonométricas
Ahora calculamos las funciones trigonométricas, empezando con $\sin(A)$:
$$ \sin(A) = \frac{\text{opuesto}}{\text{hipotenusa}} = \frac{BC}{AB} = \frac{3}{5}. $$
- Cálculo de $\cos(B)$
Para $B$, la relación es:
$$ \cos(B) = \frac{\text{adyacente}}{\text{hipotenusa}} = \frac{AC}{AB} = \frac{4}{5}. $$
- Cálculo de $\tan(A)$
Para la tangente de $A$:
$$ \tan(A) = \frac{\text{opuesto}}{\text{adyacente}} = \frac{BC}{AC} = \frac{3}{4}. $$
- Cálculo de $\tan(B)$
Para la tangente de $B$:
$$ \tan(B) = \frac{\text{opuesto}}{\text{adyacente}} = \frac{AC}{BC} = \frac{4}{3}. $$
Las afirmaciones correctas son:
- a) $\sin(A) = \frac{3}{5}$.
- b) $\cos(B) = \frac{4}{5}$.
- c) $\tan(A) = \frac{3}{4}$.
- d) $\tan(B) = \frac{4}{3}$.
More Information
Las relaciones trigonométricas se basan en las proporciones de los lados de un triángulo rectángulo. Estas proporciones se utilizan ampliamente en geometría y aplicaciones en ciencias e ingeniería. También es importante recordar que en un triángulo rectángulo, la suma de los ángulos es siempre 180 grados.
Tips
- Confundir los lados opuestos y adyacentes al calcular funciones trigonométricas.
- Olvidarse de que en un triángulo rectángulo, la hipotenusa siempre es el lado más largo.
AI-generated content may contain errors. Please verify critical information